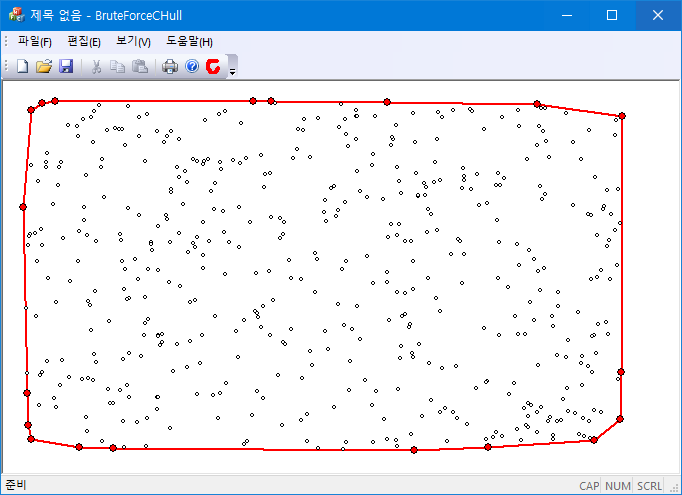
참고: http://cm.bell-labs.com/who/clarkson/2dch.c에 구현된 알고리즘을 수정함:
- 점집합을 x-좌표의 값(같으면, y좌표의 값) 순으로 정렬한다. 시작점은 hull의 꼭짓점이 된다.
- x-좌표 순서대로 현재 점이 hull의 꼭짓점인가를 검사한다: hull의 꼭짓점이 되기 위해서는 직전까지 구성된 hull의 에지 왼편에 있어야 한다. 오른편에 있으면 직전까지 구성된 hull에서 현재 점이 왼편에 놓일 때까지 꼭짓점을 제거한다.
- 남는 점들을 1번 과정의 역순으로 정렬한다. 최대 x-좌표, 최소 y-좌표점이 다시 윗 hull의 시작점이 된다.
- x-좌표가 작아지는 순서대로 2번 과정을 수행한다.
/* A->B->C가 반시계방향으로 정렬되거나(< 0), 일직선상에 있으면(=) 참이다*/
static int ccw(POINT A, POINT B, POINT C) {
int a = A.x - B.x, b = A.y - B.y, c = C.x - B.x, d = C.y - B.y;
return (a * d - b * c) <= 0; /* true if points A,B,C counterclockwise */
}static int cmpl(const void *a, const void *b) {
POINT *A = (POINT* )a, *B = (POINT* )b;
int v = A->x - B->x ; //lower-hull은 x 증가: y감소 순으로 정렬;
if (v > 0) return 1;
if (v < 0) return -1;
v = B->y - A->y ;
if (v > 0) return 1;
if (v < 0) return -1;
return 0;
}
static int cmph(const void *a, const void *b) {
return cmpl(b, a); // upper-hull은 x감소, y-증가 순으로 정렬;
}static int makeChain(POINT *V, int n, int (*cmp)(const void*, const void*)) {
qsort(V, n, sizeof(POINT), cmp);
// 꼭짓점(i(>j))가 현재까지 만들어진 hull(s까지)의 에지보다 더 오른쪽에
// 있으면(ccw(i,j,j-1)), 왼쪽에 위치할 때까지 기존 hull을 줄인다.
// 이 점을 hull에 추가.
int s = 1;
for (int i = 2; i < n; i++) {
int j = s;
while (j >= 1 && ccw(V[i], V[j], V[j - 1])) j--; // ccw의 =때문에 일직선상의
// 마지막 점만 들어감;
s = j + 1; // j = last index of hull;
// (j + 1)에 새 hull-point을 추가;
POINT t = V[i]; V[i] = V[s]; V[s] = t; // swap: V[i] <-> V[j + 1]
}
return s;
}
int chainHull(std::vector<POINT>& pts, std::vector<POINT>& chull) {
int n = pts.size();
if (n < 3) return 0;
// copy to working array;
chull.resize(n + 1);
for (int i = 0; i < n; i++) chull[i] = pts[i];
/* make lower hull */
int u = makeChain(&chull[0], n, cmpl);
/* make upper hull */
chull[n] = chull[0];
u += makeChain(&chull[u], n - u + 1, cmph);
chull.resize(u);
return u;
};
'Computational Geometry' 카테고리의 다른 글
| Catmull-Rom Spline (0) | 2020.12.07 |
|---|---|
| Incremental Delaunay Triangulation (1) | 2020.12.01 |
| Quick Hull (2) | 2012.09.16 |
| Monotone Cubic Interpolation (0) | 2012.09.09 |
| Brute Force Convex Hull Algorithm (0) | 2012.09.06 |