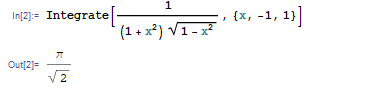복소함수
을 그림과 같은 contour에 대해서 적분을 한다. $f(z)$는 $z=0, 1$이 branch point이므로 그림처럼 branch cut을 선택한다.
$C_1$에서
이므로
$C_3$에서
이므로
그리고, $C_2, C_4$에서 $$\int f(z) = O(\sqrt{\epsilon}) \rightarrow 0$$이므로
'Mathematics' 카테고리의 다른 글
| 주어진 길이의 폐곡선으로 가둘 수 있는 최대 면적의 도형은? (0) | 2020.02.15 |
|---|---|
| Integration along a branch cut-005 (0) | 2017.07.02 |
| Integration along a branch cut-003 (0) | 2017.06.28 |
| Integration along a branch cut-002 (1) | 2017.06.28 |
| Integration along a branch cut-001 (0) | 2017.06.27 |