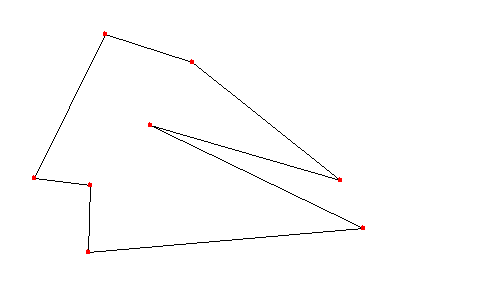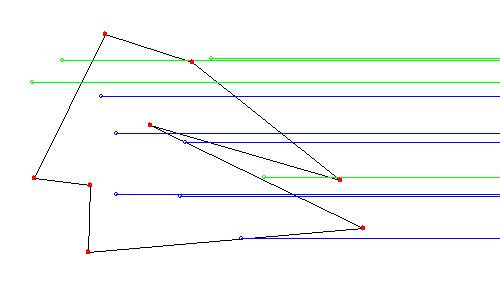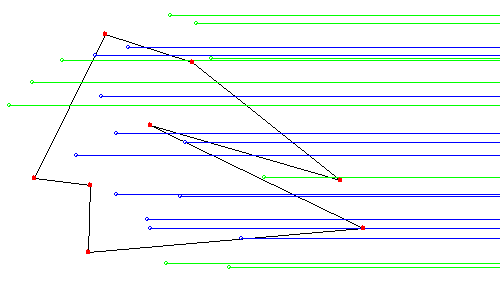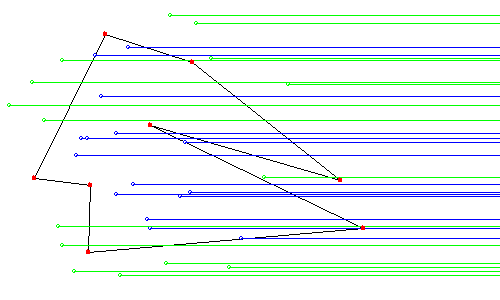
기하 관련 프로그래밍을 하다 보면 평면 상의 한 점이 다각형 내의 점인가 아니면 밖의 점인가를 판단해야 할 필요성이 많이 생긴다. 이 문제에 대한 답을 생각해보기로 하자. $N$개의 꼭짓점 $\{ x_i, y_i| i=0,...., N-1\}$으로 구성이 된 다각형을 놓고 생각을 하도록 하자. 평면상의 주어진 점 $(x_p, y_p)$에서 오른쪽으로 출발하는 반직선을 쭉 그으면 다각형과 교차하는 점들이 생기게 된다. 교차하는 상황을 잘 헤아려 보면 해당점이 다각형의 내부에 들어 있는 경우에는 항상 홀수번의 교차점이 생기고, 외부에 있는 경우에는 짝수번(0번 포함)의 교차점이 생김을 알 수 있다. 따라서 주어진 점에서 시작하는 반직선과 다각형의 교차점 개수의 홀짝 여부를 판별하면 내부/외부점인지에 대한 문제를 풀 수 있다. 여기서 한 가지 주의할 사항은, 주어짐 점에서 그은 반직선이 다각형의 변(edge)을 포함하는 경우는 제외해야 하고, 꼭짓점이 반직선에 걸리는 경우는 꼭짓점을 공유하는 두 변과 만나지만 한 번으로 카운트해야 한다.
** 주의: 경계점(+꼭지점)에 대한 처리는 일관성이 있는 결과를 주지 않는다.
BOOL is_inside_polygon(POINT p, POINT polygon[], int N) {
int counter = 0;
POINT* q1 = &polygon[0];
for (int i = 1; i <= N; i++) {
POINT *q2 = &polygon[i % N];
if (p.y > min(q1->y, q2->y)) { //y-intersect.;
if (p.y <= max(q1->y, q2->y)) { //y-intersect(=single);
if (p.x <= max(q1->x, q2->x)) //x-intersect;
if (q1->y != q2->y) { //not parallel;
double xq = double(p.y - q1->y) * (q2->x - q1->x) / (q2->y - q1->y) + q1->x;
// x-intersect;
if (q1->x == q2->x || p.x <= xq)
counter++;
}
}
}
}
q1 = q2; // move to next edge;
}
return (counter % 2);
}
참고:
728x90
'Computational Geometry' 카테고리의 다른 글
| 단순 다각형의 면적(2D) (0) | 2021.01.23 |
|---|---|
| 삼각형 외접원의 Inclusion Test (0) | 2020.12.30 |
| Catmull-Rom Spline (0) | 2020.12.07 |
| Incremental Delaunay Triangulation (1) | 2020.12.01 |
| Chain Hull (2) | 2012.09.16 |




