이미지 처리에서 픽셀 좌표는 간격이 1인 2차원 그리드의 교차점으로 볼 수 있다. 이미지를 확대하거나 축소할 때, 픽셀과 픽셀 사이 구간에서 값이 필요한 경우가 생긴다. 간단하게는 가장 가까운 주변 픽셀의 값을 그대로 가져다 쓰거나, 또는 주변의 4 픽셀 값을 선형보간해서 사용할 수 있다. 2차원 그리드에서 선형보간은 bilinear interpolation이다. 이 보간법은 속도는 빠르지만 픽셀 값이 인접 그리드에서의 값으로 부드럽게 이어지지 않는 단점이 있다. 인접 그리드 경계에서 픽셀 값이 부드럽게 이어지기 위해서는 적어도 1차 미분이 연속인 보간법을 사용해야 하는데, 이러한 조건을 만족시키는 가장 낮은 찾수의 다항식 보간법이 bicubic interpolation이다.
4점 $(0,0), (0,1), (1,0),(1,1)$을 꼭짓점으로 하는 정사각형 내의 임의 지점 $D=\{(x, y)| 0 \le x\le1, 0\le y \le 1\}$ 에서 픽셀 값을 주는 보간곡면 $f(x, y)$을 주변의 16개 점 $\{(i, j)| -1 \le i \le 2, -1 \le j \le 2\}$에서 픽셀 값을 사용하는 bicubic interpolation을 이용해서 추정할 수 있다. 곡면 $f(x, y)$은 $x$와 $y$의 3차 함수로 다음과 같이 쓸 수 있다.
\begin{align} f(x, y)= \sum_{i=0}^{3} \sum_{j=0}^{3} a_ {ij} x^i y^j. \end{align}
문제는 16개 계수 $\{a_{ij}\}$를 어떻게 찾을 것인가? 이를 위해 16개의 조건이 필요한데 주변의 16개의 픽셀 값을 이용해서 만들 수 있다. 또한 픽셀 값이 인접 그리드 영역으로 smooth 하게 연결되기 위해서는 $f(x, y)$의 미분도 고려해야 한다.
- 4 꼭짓점에서 값 $f(x,y)$: \begin{align}f(0,0)& = a_{00};\\ f(1,0)& = a_{00} + a_{10} + a_{20} + a_{30}; \\ f(0,1) &= a_{00} + a_{01} + a_{02} + a_{03};\\ f(1,1) &= a_{00} + a_{10} + a_{20} + a_{30} + a_{01} + a_{11} + a_{21} + a_{31} \\ &+ a_{02} + a_{12} + a_{22} + a_{32} + a_{03} + a_{13} + a_{23} + a_{33};\end{align}
- 4 꼭짓점에서 미분계수, $f_x$, $f_y$: \begin{align} f_x(0,0) &= a_{10} ; \\ f_x(1,0) &= a_{10} + 2 a_{20} + 3 a_{30} ; \\ f_x(0,1) &= a_{10} + a_{11} + a_{12} + a_{13}; \\ f_x(1,1) &= a_{10} + 2 a_{20} + 3 a_{30} + a_{11} + 2 a_{21} + 3 a_{31} \\ &+ a_{12} + 2a_{22} + 3a_{32} + a_{13} + 2a_{23} + 3a_{33};\\ f_y(0,0)&=a_{01} \\ f_y(1,0) &= a_{01} + a_{11} + a_{21} + a_{31};\\ f_y(0,1) &= a_{01} + 2a_{02} + 3a_{03}; \\ f_y(1,1) &= a_{01} + a_{11} + a_{21} + a_{31} + 2 a _{02} + 2 a_{12} + 2 a_{22} + 2 a_{32} \\&+ 3a_{03} + 3a_{13} + 3a_{23} + 3a_{33};\end{align}
- 4 꼭짓점에서 교차 미분계수, $f_{ij}$: \begin{align} f_{xy} (0,0)& = a_{11}; \\ f_{xy}(1,0)& = a_{11} + 2a_{21} + 3a_{31}; \\ f_{xy}(0,1)& = a_{11} + 2a_{12} + 3a_{13}; \\ f_{xy}(1,1) &= a_{11} + 2a_{21} + 3a_{31} +2a_{12} + 4a_{22} \\ &+ 6a_{32} + 3a_{13} + 6a_{23} + 9a_{33};\end{align}
꼭짓점에서 $f(x, y)$의 미분계수는 꼭짓점과 인접 교차점 사이의 평균 변화율로 표현할 수 있다. 주변의 픽셀이 $p [i+1, j+1] = f(i,j)$로 주어진 경우;
\begin{align} f_{00}&=p[1,1], f_{10}=p[2,1], ...\\f_{x00} &=f_x(0,0) = \frac{1}{2} (f(1,0)-f(-1,0))=\frac{1}{2}(p [2,1] -p [0,1]),... \\ f_{xy00} &= f_{xy}(0,0) = \frac{1}{4}( f(1,1)-f(1,-1)-f(-1,1)+f(-1,-1) )\\&=\frac{1}{4}(p[2,2]-p[2, 0]-p[0,2]+p[0,0]),...\end{align}
와 같다.
위의 식들은 16개의 미지수 {$a_{ij} $}를 가지는 16개의 연립 방정식이므로 이를 풀어서 계수를 구할 수 있다. 계수를 벡터 ${\mathbf v}$로
$$\mathbf{v} = [ a_{00}, a_{10}, a_{20},a_{30},a_{01},a_{11},a_{21},a_{31},a_{02},a_{12},a_{22},a_{32},a_{03},a_{13}, a_{23},a_{33}]^t$$
로 나타내고, 각 꼭짓점에서의 픽셀 값, 미분 값을 ${\mathbf f}$ 벡터로 나타내면
$$\mathbf{f} = [f_{00}, f_{10},f_{01},f_{11}, f_{x00}, f_{x10},f_{x01}, f_{x11}, f_{y00}, f_{y10}, f_{y01}, f_{y11}, f_{xy00}, f_{xy10}, f_{xy01}, f_{xy11}]^t.$$
16개의 연립 방정식은 행렬식
$${\bf f} ={\mathbf A} \cdot {\mathbf v}\quad(해: {\mathbf v}={\mathbf A} ^{-1} \cdot {\mathbf f}) $$
으로 쓸 수 있다. 여기서,
$$\mathbf {A}= \left( \begin {array}{cccccccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 2 & 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 2 & 3 & 0 & 1 & 2 & 3 & 0 & 1 & 2 & 3 & 0 & 1 & 2 & 3 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 2 & 2 & 2 & 2 & 3 & 3 & 3 & 3 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 2 & 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 2 & 3 & 0 & 2 & 4 & 6 & 0 & 3 & 6 & 9 \\ \end {array}\right)$$
그리고 역행렬은
$$\mathbf {A}^{-1}=\left(\begin {array}{cccccccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -3 & 3 & 0 & 0 & -2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & -2 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -3 & 3 & 0 & 0 & -2 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & -2 & 0 & 0 & 1 & 1 & 0 & 0 \\ -3 & 0 & 3 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -3 & 0 & 3 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & -1 & 0 \\ 9 & -9 & -9 & 9 & 6 & 3 & -6 & -3 & 6 & -6 & 3 & -3 & 4 & 2 & 2 & 1 \\ -6 & 6 & 6 & -6 & -3 & -3 & 3 & 3 & -4 & 4 & -2 & 2 & -2 & -2 & -1 & -1 \\ 2 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ -6 & 6 & 6 & -6 & -4 & -2 & 4 & 2 & -3 & 3 & -3 & 3 & -2 & -1 & -2 & -1 \\ 4 & -4 & -4 & 4 & 2 & 2 & -2 & -2 & 2 & -2 & 2 & -2 & 1 & 1 & 1 & 1 \\ \end {array}\right)$$
이 역행렬은 mathematica나 maple 등의 프로그램을 이용하면 쉽게 구할 수 있다. 이렇게 구한 $f(x, y)$는 $[0,1]\times [0,1]$ 영역에서 연속인 smooth 한 곡면을 형성한다. 또한 인접하는 그리드 영역의 곡면과 경계에서 smooth 하게 연결된다.
/* 픽셀의 위치가 grid의 교차점이 되도록 표현하였다*/

/* [ix, ix+1][iy, iy+1] 영역에서 보간을 하는 경우에, 주변 픽셀의 정보는
** p[a][b]에 들어가고, p[a][b]= Image (ix - 1 + a, iy - 1 + b)
** 0 <= x < 1, 0 <= y < 1
*/
double BicubicInterpolate(double p[4][4], double x, double y) {
double a00 = p[1][1];
double a01 = -.5*p[1][0] + .5*p[1][2];
double a02 = p[1][0] - 2.5*p[1][1] + 2*p[1][2] - .5*p[1][3];
double a03 = -.5*p[1][0] + 1.5*p[1][1] - 1.5*p[1][2] + .5*p[1][3];
double a10 = -.5*p[0][1] + .5*p[2][1];
double a11 = .25*p[0][0] - .25*p[0][2] - .25*p[2][0] + .25*p[2][2];
double a12 = -.5*p[0][0] + 1.25*p[0][1] - p[0][2] + .25*p[0][3] +
.5*p[2][0] - 1.25*p[2][1] + p[2][2] - .25*p[2][3];
double a13 = .25*p[0][0] - .75*p[0][1] + .75*p[0][2] - .25*p[0][3] -
.25*p[2][0] + .75*p[2][1] - .75*p[2][2] + .25*p[2][3];
double a20 = p[0][1] - 2.5*p[1][1] + 2*p[2][1] - .5*p[3][1];
double a21 = -.5*p[0][0] + .5*p[0][2] + 1.25*p[1][0] - 1.25*p[1][2] -
p[2][0] + p[2][2] + .25*p[3][0] - .25*p[3][2];
double a22 = p[0][0] - 2.5*p[0][1] + 2*p[0][2] - .5*p[0][3] - 2.5*p[1][0] +
6.25*p[1][1] - 5*p[1][2] + 1.25*p[1][3] + 2*p[2][0] - 5*p[2][1] +
4*p[2][2] - p[2][3] - .5*p[3][0] + 1.25*p[3][1] - p[3][2] + .25*p[3][3];
double a23 = -.5*p[0][0] + 1.5*p[0][1] - 1.5*p[0][2] + .5*p[0][3] + 1.25*p[1][0] -
3.75*p[1][1] + 3.75*p[1][2] - 1.25*p[1][3] - p[2][0] + 3*p[2][1] -
3*p[2][2] + p[2][3] + .25*p[3][0] - .75*p[3][1] + .75*p[3][2] - .25*p[3][3];
double a30 = -.5*p[0][1] + 1.5*p[1][1] - 1.5*p[2][1] + .5*p[3][1];
double a31 = .25*p[0][0] - .25*p[0][2] - .75*p[1][0] + .75*p[1][2] +
.75*p[2][0] - .75*p[2][2] - .25*p[3][0] + .25*p[3][2];
double a32 = -.5*p[0][0] + 1.25*p[0][1] - p[0][2] + .25*p[0][3] + 1.5*p[1][0] -
3.75*p[1][1] + 3*p[1][2] - .75*p[1][3] - 1.5*p[2][0] + 3.75*p[2][1] -
3*p[2][2] + .75*p[2][3] + .5*p[3][0] - 1.25*p[3][1] + p[3][2] - .25*p[3][3];
double a33 = .25*p[0][0] - .75*p[0][1] + .75*p[0][2] - .25*p[0][3] - .75*p[1][0] +
2.25*p[1][1] - 2.25*p[1][2] + .75*p[1][3] + .75*p[2][0] - 2.25*p[2][1] +
2.25*p[2][2] - .75*p[2][3] - .25*p[3][0] + .75*p[3][1] -
.75*p[3][2] + .25*p[3][3];
double x2 = x * x;
double x3 = x2 * x;
return a00 + (a01 + (a02 + a03 * y) * y) * y +
(a10 + (a11 + (a12 + a13 * y) * y) * y) * x +
(a20 + (a21 + (a22 + a23 * y) * y) * y) * x2 +
(a30 + (a31 + (a32 + a33 * y) * y) * y) * x3;
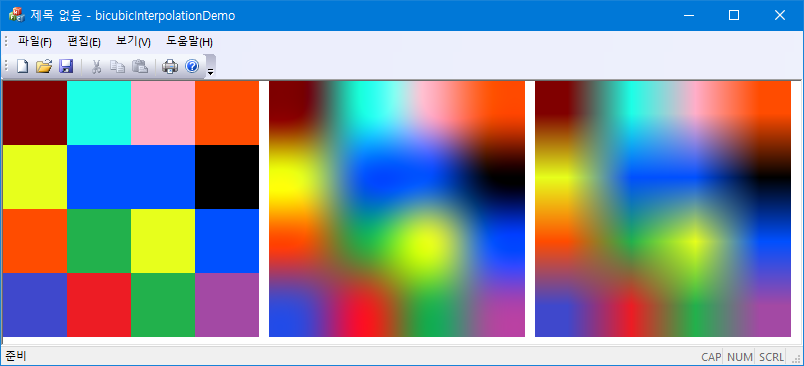
};* 원본 4x4 이미지(RGB): nearest-neighbor interploation으로 256x256 크기로 만듦;

* bicubic interpolation 결과 (256x256):

* bilinear interpolation 결과 (256x256):

코드 구현 일부: bicubic interpolation은 주변의 16개 픽셀 정보가 필요한데, 가장자리 픽셀인 경우는 이를 충족시킬 수 없으므로 이를 해결하기 위해 영역 밖은 가장자리 픽셀이 반복된 것으로 처리하는 것이 가장 쉽다. 그리고 소스 영상이 큰 경우에는 문제가 되지 않지만 예제처럼 작은 소스 영상의 경우는 가장자리 부근에서 단순 채움을 사용하면 왜곡이 발생한다. 이를 해소하기 위해서는 소스 픽셀 위치가 픽셀의 중간을 나타낸 것으로 처리하면 된다.
'Image Recognition > Fundamental' 카테고리의 다른 글
| Otsu-알고리즘의 새로운 해석 (0) | 2010.01.28 |
|---|---|
| Object Orientation (1) | 2010.01.17 |
| Bezier Curve을 이용한 Histogram Smoothing (0) | 2010.01.10 |
| Running Median Filter (0) | 2010.01.07 |
| Fant's Resampling (0) | 2008.12.17 |




