Geometry & Recognition

$$I = \int_{-\infty}^\infty \frac{p e^{ipr} dp}{\sqrt{p^2 + m^2 }  } \quad   (r>0,~m>0)$$

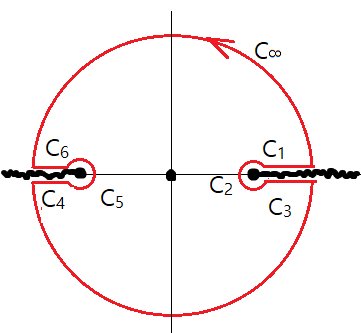
복소함수 $f(z) =\frac{z e^{izr} }{\sqrt{z^2 + m^2}}$을 contour 적분을 이용한다. $z=\pm im$가 $f(z)$의 branch point이므로 그림과 같이 cut line을 잡는다(적분은 upper half plane에서 한다). $z=im$ 근방에서 위상은 $-3\pi/2\rightarrow \pi/2$로 선택한다.

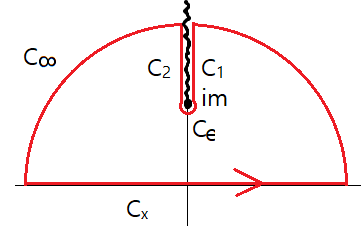
그림의 contour에서 $f(z)$가 analytic하므로 $\int_\Gamma f(z) dz = 0$이고,

$C_1$: $z-im = (s-m) e^{i \pi/2} ~~(s: \infty\rightarrow m)$, $z+im = (s+m) e^{i\pi/2}$, $z=is$이므로

$$\int_{C_1} f(z) dz = \int_{\infty}^m \frac{  (is) e^{-sr} (ids)}{ \sqrt{s^2 - m^2 } e^{i\pi/2}} = -i \int_m^\infty \frac{s e^{-sr} ds }{ \sqrt{ s^2 - m^2}} .$$

$C_2$: $z-im= (s-m) e^{-i 3\pi/2} ~~(s: m\rightarrow \infty)$, $z+im = (s+m) e^{i \pi/2}$, $z=is$이므로

$$\int_{C_2} f(z) dz = \int_m^\infty \frac{ (is) e^{-sr} (ids) }{ \sqrt{s^2 - m^2 }} e^{-i \pi /2} = -i \int_m^\infty \frac{s e^{-sr}ds }{\sqrt{s^2 - m^2} }.$$

그리고 $$ \int_{C_\epsilon} f(z) dz  = O( \sqrt{\epsilon})\rightarrow 0.$$

$C_\infty$에서 $z=R e^{i\theta} ~(\theta:0\rightarrow \pi)$로 놓으면 $|e^{izr}|  \le  e^{- R \sin \theta r} \rightarrow 0$이므로 

$$\int_{C_\infty} f(z) dz \rightarrow 0.$$

따라서 $x$-축을 따라 적분한 값 $I$는

$$I = \int_{-\infty}^{\infty} \frac{p e^{i p r}dp}{ \sqrt{p^2 + m^2 }} = 2i \int_m^\infty \frac{se^{-sr} ds} {\sqrt{s^2 - m^2}} =i\times \text{positive number}.$$ 우변의 적분은 closed form으로 표현이 안되지만 0이 아님은 알 수 있다. 그리고 실함수에 대한 적분이므로 수치적으로 계산하기 쉬운 형태로 바뀐 것이다.

$$I = \int_1^\infty \frac{dx}{x\sqrt{x^2-1}}$$

복소 함수 $f(z)= \frac{1}{z\sqrt{z^2-1}}$의 contour 적분을 이용해서 구한다. $z =\pm 1$이 branch point이므로 branch cut을 그림처럼 잡는다.

$z=+1$의 근방에서 위상은 $0\rightarrow 2\pi$, $z=-1$에서는 $-\pi \rightarrow \pi$로 선택한다.  $z=0$이 simple pole이므로 

$$ \int_\Gamma f(z) dz = 2\pi.$$

$C_1$:   $z= x e^{i0}~(x: 1 \rightarrow \infty)$, $z-1=(x-1)e^{i0}$, $z+1 = (x+1)e^{i0}$이므로

$$\int_{C_1} f(z)dz = I$$

$C_3$: $z= x e^{i2\pi }~(x:\infty \rightarrow 1)$, $z-1=(x-1)e^{i2\pi }$, $z+1 = (x+1)e^{i0}$이므로

$$\int_{C_3} f(z)dz = \int_\infty^1 \frac{d}{x\sqrt{x^2-1} e^{i\pi}   } = I. $$

$C_4$: $z= x e^{i \pi }~(x:1 \rightarrow \infty)$, $z-1=(1+ x)e^{i\pi }$, $z+1 = (x-1)e^{-i \pi}$이므로

$$\int_{C_4} f(z)dz = \int_1^\infty \frac{d}{(-x)\sqrt{x^2-1}   } = I. $$

$C_6$: $z= x e^{i\pi}~(x: \infty \rightarrow 1)$, $z-1=(1+ x)e^{i\pi }$, $z+1 = (x-1)e^{i \pi}$이므로

$$\int_{C_6} f(z)dz = \int_\infty^1 \frac{-dx}{(-x)\sqrt{x^2-1}e^{i\pi}   } = I. $$

그리고,

$$\int_{C_2} f(z)dz = \int_{C_5} f(z) dz = O(\sqrt{\epsilon}) \rightarrow 0 \\ \int_{C_\infty} f(z)dz =  O( 1/R) \rightarrow 0$$

이므로

$$ I = \int_1^\infty \frac{dx}{x \sqrt{x^2-1} } = \frac{\pi }{2}.$$