Geometry & Recognition

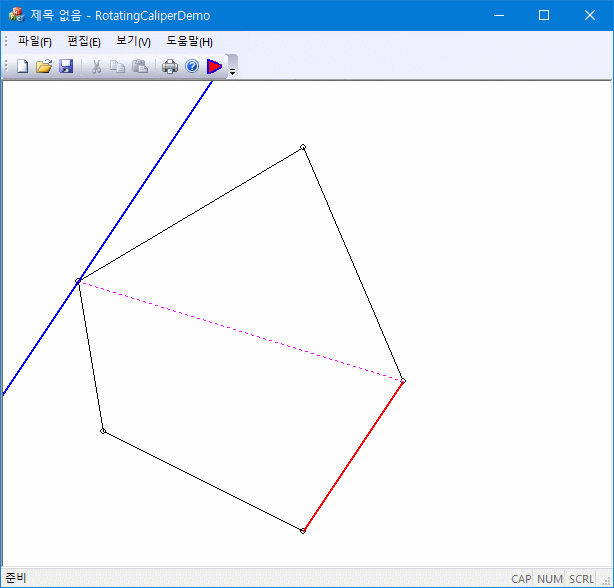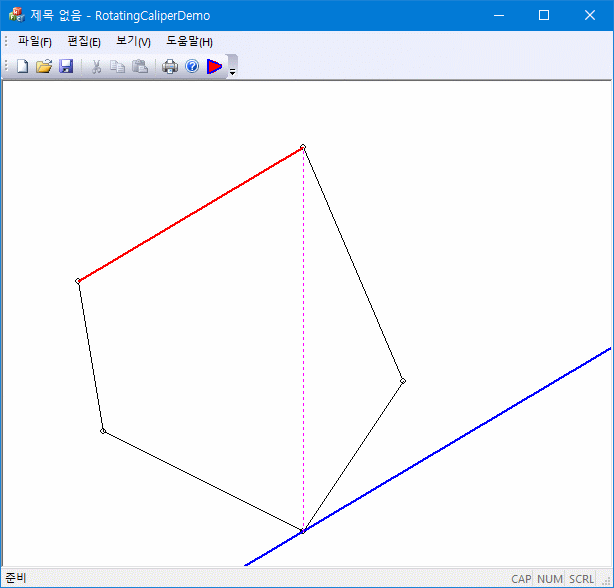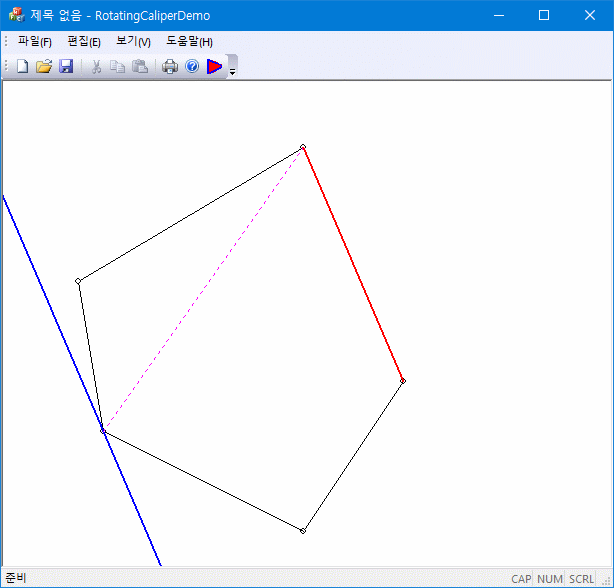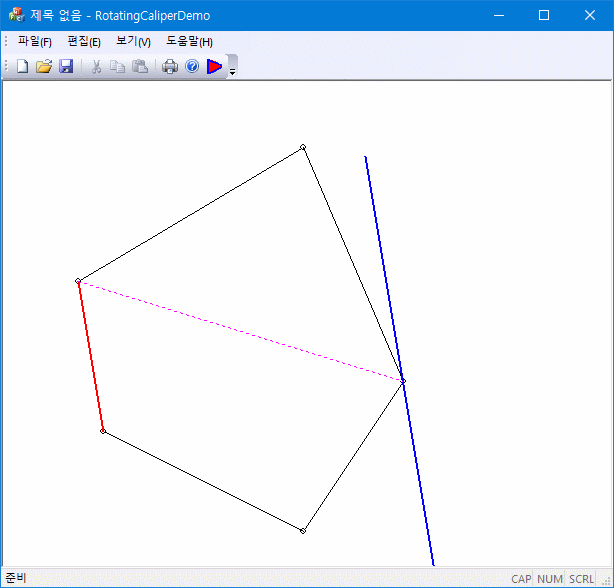
볼록 다각형(convex polygon)에서 한 방향으로(예를 들면 y-축방향) 가장 멀리 떨어진 두 꼭짓점(antipodal points) 통과하는 평행한 두 직선을 생각해보자. 평행 직선의 방향은 이 경우에는 x-축(y-축과 수직)과 나란해야 한다. 이제 두 평행 직선의 방향을 각각의 꼭짓점을 축으로 해서 조금씩 회전시키면, 둘 중 하나는 볼록 다각형에 먼저 접하게 된다. 이 접하는 변을 기준으로 다시 antipodal point을  찾아 (당연히 접하지 않는 평행직선이 통과하는 꼭짓점이 된다) 새로운 평행 직선을 구성한 후 동일한 과정을 반복한다. 이 과정을 N회 반복하면 볼록 다각형의 모든 변에 대해서 변을 공유하는 직선과 그 직선의 antipodal point를 찾을 수 있다. 

이 rotating calipers를 이용하면 convex hull의 bounding box, convex hull의 diameter, convex polygon 사이 거리 등의 계산에 응용할 수 있다.

double COS(CPoint A, CPoint B) {             // directional cosine;
    double norm2A = A.x * A.x + A.y * A.y;
    double norm2B = B.x * B.x + B.y * B.y;
    return (A.x * B.x + A.y * B.y) / sqrt(norm2A * norm2B);
}
int ccw(CPoint A, CPoint B, CPoint C) {     // cross(AB, BC); 반시계방향 > 0;
    return (B.x - A.x) * (C.y - B.y) - (B.y - A.y) * (C.x - B.x) ;
}
// find antipodal points along y-direction;
bool initCalipers(std::vector<CPoint> &Q, 
                 int &minid, double &minCos,
                 int &maxid, double &maxCos) {
    int N = Q.size();
    // ccw check (중복 // 일직선을 고려);
    int orient = 0;
    for (int i = 0; i < N; i++) {
        orient = ccw(Q[(i - 1 + N) % N], Q[i], Q[(i + 1) % N]);
        if (orient != 0) break;
    }
    if (orient == 0) return false;

    minid = maxid = 0;
    for (int i = 1; i < N; i++) {
        if (Q[i].y < Q[minid].y) minid = i;
        if (Q[i].y > Q[maxid].y) maxid = i;
    }

    CPoint n0 = CPoint(1, 0);
    if (orient < 0) n0 = -n0;  // convex hull이 CW인 경우;
    CPoint dir0 = Q[(minid + 1) % N] - Q[minid];
    CPoint dir1 = Q[(maxid + 1) % N] - Q[maxid];
    minCos = COS(dir0, n0);
    maxCos = COS(dir1, -n0);
    return true;
}
int rotatingCalipers(std::vector<CPoint> &Q,
                    int &i0, double &dirCos0,
                    int &i1, double &dirCos1) {
    int N = Q.size();
    int i0next = (i0 + 1) % N ;
    int i1next = (i1 + 1) % N ;
    CPoint dir0 = Q[i0next] - Q[i0];
    CPoint dir1 = Q[i1next] - Q[i1];
    if (dirCos0 > dirCos1) {          // i0을 포함하는 평행선이 다음 edge와 이루는 각이 작음;
        CPoint ndir0 = Q[(i0next + 1) % N] - Q[i0next]; // 각을 재는 기준선은 현재 다다음 edge;
        dirCos0 = COS(ndir0, dir0);    
        dirCos1 = COS(dir1, -dir0);    
        i0 = i0next;                  // i0는 다음 꼭지점으로 이동; i1 = antipodal point;
        return 0;
    } else {                          // i1을 포함하는 평행선이 다음 edge와 이루는 각이 작음
        CPoint ndir1 = Q[(i1next + 1) % N] - Q[i1next];
        dirCos1 = COS(ndir1, dir1);   
        dirCos0 = COS(dir0, -dir1);   
        i1 = i1next;                  // i1은 다음 꼭지점으로 이동; i0 = antipodal point;
        return 1;
    }
}
void runCalipers(std::vector<CPoint> &Q) {
    int i0, i1;
    double dirCos0, dirCos1;
    bool done = false;
    if (!initCalipers(Q, i0, dirCos0, i1, dirCos1)) return ;  // fails
    while (!done) {
    	int i0old = i0, i1old = i1;
        if (rotatingCalipers(Q, i0, dirCos0, i1, dirCos1) == 0) {
            // Q[i1] = antipodal point;
            // do something useful...
        } else {
            // Q[i0] = antipodal point;
            // do something useful...
        }
    }
};

2차원 점집합의 median

• www.cs.princeton.edu/~chazelle/pubs/ConvexLayers.pdf
• arxiv.org/ftp/arxiv/papers/1803/1803.04964.pdf

Convex hull을 찾을 때, 중복점과 일직선상 위에 있는 점들에 대해서 적절한 처리를 하지 않으면 효율적으로 작성된 알고리즘이라도 정상적으로 동작하지 않을 수 있다. 그림은 Graham Scan 알고리즘을 이용해서 50,000개 점들의 convex hull을 구한 결과다. qsort()을 호출할 때 compare()에서 global 변수를 쓰지 않기 위해서 pivot point를 뺀 후 사용한다. 정렬 후에는 다시 더해준다.

inline int LeftSide(CPoint A, CPoint B, CPoint C) {
    return (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y); // cross(AB, AC);
}
static int cross(CPoint *p1, CPoint *p2) {
    return p1->x * p2->y - p1->y * p2->x;
}
static int norm2(CPoint *p) {
    return p->x * p->x + p->y * p->y;
}
static int compare(const void *a, const void *b) {
    CPoint *p1 = (CPoint *)a, *p2 = (CPoint *)b;
    int ccw = cross(p2, p1);
    // 거리가 먼 곳 --> 가까운 곳;
    if (ccw == 0) return norm2(p2) > norm2(p1) ? 1 : -1;
    return ccw; // 반시계방향 정렬;
}
static void angularSort(std::vector<CPoint> & pts) {
    if ((pts.size()) < 2) return;
    int id = 0;
    for (int i = pts.size() - 1; i >= 1; --i) 
        if ((pts[id].y > pts[i].y) || (pts[id].y == pts[i].y && pts[i].x > pts[id].x)) 
            id = i;  //lowest--y-value; //largest--x-value;
    std::swap(pts[0], pts[id]);
    for (int i = pts.size() - 1; i >= 1; --i) pts[i] -= pts[0];
    qsort(&pts[1], pts.size() - 1, sizeof(CPoint), compare);
    for (int i = pts.size() - 1; i >= 1; --i) pts[i] += pts[0];
};
// AB와 BC가 나란할 때, AB 방향과 BC방향이 같은가(0) 반대면 (1): dot(AB, BC);
static int folded(CPoint A, CPoint B, CPoint C) {
    return (B.x - A.x) * (C.x - B.x) + (B.y - A.y) * (C.y - B.y) <= 0;
}
int GrahamScan(std::vector<CPoint>& pts, std::vector<CPoint>& hull) {
    if (pts.size() < 3) return 0;
    angularSort(pts);
    hull.resize(pts.size());
    hull[0] = pts[0];
    int i = 1; 
    while (i < pts.size()) { 
        // peek out points degenerate with pts[0];
        if (pts[i] != hull[0]) {
            hull[1] = pts[i++]; break;  //  (i++)
        }
        i++;
    }
    if (i == pts.size()) return 0;
    int k = 2; // 새로 추가되는 hull index;
    while (i < pts.size()) {
        // (i)가 hull의 left에 있으면(1) hull의 꼭지점에 추가;
        int ccw = LeftSide(hull[k - 2], hull[k - 1], pts[i]); 
        if (ccw > 0) hull[k++] = pts[i++];
        // (i)가 hull의 직전 변과 collinear한 데 반대방향을 향하면 skip;
        else if (ccw == 0 && folded(hull[k - 2], hull[k - 1], pts[i])) ++i;
        // (i)가 hull의 right 또는 위에 있으면(직전 변과 같은 방향)
        // hull의 직전 꼭지점을 순차적으로 제거한 후 다시 검사;
        else --k;
        ASSERT(k >= 2);
    }
    hull.resize(k);
    return hull.size();
};

기하 알고리즘에서 입력점의 개수가 많아지면 중복점이 생기고, 이 때문에 최적화에 주안점을 둔 알고리즘은 중복점에 대한 예외처리를 하지 않으면 정상적으로 동작하지 않는 경우가 종종 생긴다. 안정성과 구현의 간결함을 유지하고 싶으면 좀 더 brute force method에 가까운 알고리즘을 사용하는 것도 고려해 볼 수 있다. 다음은 Jarvis March 알고리즘을 써서 2차원 convex hull을 구하는 코드이다. (그림은 50,000개의 입력점을 사용함.)

BOOL ccw(CPoint a, CPoint b, CPoint c){	
    // cross(ac, ab) < 0: ab가 ac보다 오른쪽에 있음 = b가 ac변의 오른쪽에 있음.
    return ((c.x - a.x) * (b.y - a.y) - (c.y - a.y) * (b.x - a.x)) < 0;
}
int JarvisMarch(std::vector<CPoint> &pts, std::vector<CPoint> &hull) {
    int n = pts.size();
    if (n < 3) return 0;
    int left = 0;
    for (int i = 1; i < n; i++) //convex hull의 첫번째는 맨 왼쪽 점;
        if (pts[i].x < pts[left].x) left = i;
    hull.clear();
    int turns = 0; //debug 용도
    int prev = left;
    while (1) {
        hull.push_back(pts[prev]);
        int next = (prev + 1) % n;
        // prev-next 변이 모든 점의 오른쪽에 있게 하는 next를 찾으면 됨;
        // 없으면 next가 convex hull 위의 점임; 
        for (int i = 0; i < n; i++) {
            if (i == next || i == prev) continue;
            if (ccw(pts[prev], pts[i], pts[next]))  
                next = i;
        }
        prev = next;
        turns++;     //debug 용도;
        if (prev == left) break;
    } 
    TRACE("number of turns = %d\n", turns);
    remove_collinear(hull); // removes collinear vertices(optional);
    return hull.size();
}

int remove_collinear(std::vector<CPoint>& V) {
    int N = V.size();
    if (N < 3) return 0;
    // 먼저, 일직선상에 있지 않는 vertex을 찾음;
    int start; 
    for (start = 0; start < N; start++)
        if (ccw(V[(start - 1 + N) % N], V[start], V[(start + 1) % N]))
            break;

    std::vector<CPoint> H;
    H.push_back(V[start]);
    int prev = start;
    int curr = (prev + 1) % N;
    int next = (curr + 1) % N;
    while (curr != start) {
        if (ccw(V[prev], V[curr], V[next])) {
            H.push_back(V[curr]);
            prev = curr;
        } 
        curr = (curr + 1) % N;
        next = (curr + 1) % N;
    }
    std::swap(V, H);
    return V.size();
};

$$\underset{q \in P}{\text{max}}~|q - c| \le (1+\epsilon)R_P$$

$\epsilon=0.1$ (red=exact MEB)인 경우;

void ApproxMinBall(std::vector<CPoint> &pts, double epsilon, CfPt &center, double &radius) {
    double epsilonsq = epsilon * epsilon;
    int maxiters = int( 1 / epsilonsq );
    double maxdist2 = 0;
    int id = rand() % pts.size();
    center.x = pts[id].x; 
    center.y = pts[id].y;
    for (int iter = 0; iter < maxiters; iter++) { 
        // find the furthest point from (cx, cy);
        maxdist2 = 0;
        id = 0;
        for (int i = pts.size(); i-- > 0;) {
            double dx = pts[i].x - center.x, dy = pts[i].y - center.y;
            double dist2 = dx * dx + dy * dy;
            if (dist2 > maxdist2) {
                maxdist2 = dist2;
                id = i;
            }
        }
        // update center;
        center.x += (pts[id].x - center.x) / iter;
        center.y += (pts[id].y - center.y) / iter;
    }
    radius = sqrt(maxdist2);
}

kipl.tistory.com/300