Geometry & Recognition

Fixed-point version: 선분 길이가 4096 픽셀 정도까지는 1-pixel 이내의 오차로 그려진다.

void DDALine(CPoint A, CPoint B) {
    const int mulfac = 4096; // 2^12 = 4096;
    int dx = B.x - A.x;
    int dy = B.y - A.y;
    int adx = dx < 0 ? -dx : dx;
    int ady = dy < 0 ? -dy : dy;
    int steps = adx < ady ? ady : adx;
    if (steps == 0) SetPixel(A.x, A.y); //single point;
    else {
        int curX = A.x * mulfac;      
        int curY = A.y * mulfac;
        dx = (dx * mulfac) / steps;
        dy = (dy * mulfac) / steps;
        while (steps-- >= 0) {
            SetPixel(curX / mulfac, curY / mulfac);
            curX += dx;
            curY += dy;
        }
    }
}

$$ \mathbf{C}(u) = \sum_{i=0}^{n} N_{i,p} (u) \mathbf{P}_i$$

where $N_{i, p}(u)$'s are B-spline basis functions of degree $p$, $n+1$ control points $\{\mathbf{P}_i\}$, and a knot vector $\mathbf{U}=(u_0, u_1, ..., u_m)$. Note, $m=n + p + 1$.

B-spline의 basis 함수 $N_{i, p}(t)$는 유한한 구간에서만 0이 아닌 값을 갖는(local support) 함수로 다음과 같은  recursion relation을 가진다:

\begin{align} N_{i,0}(t) &= \left\{ \begin{matrix} 1 & \mathrm{if} \quad u_i \leq x \lt u_{i+1} \\ 0 & \mathrm{otherwise} \end{matrix} \right. \quad \quad (0 \le i \le n+p), \\ N_{i,p}(t) &= \frac{t - u_i}{u_{i+p} - u_i} N_{i,p-1}(t) + \frac{u_{i+p+1} - t}{u_{i+p+1} - u_{i+1}} N_{i+1,p-1}(t).\end{align}

$N_{i,p}(t)$의 local support는 $[u_i, u_{i+p+1}]$로 주어진다.

일반적으로 knot vector가 특별한 구조를 가지지 않으면 B-spline곡선은 Bezier 곡선의 경우와 달리 처음과 끝 control 점을 통과하지 않는다(open B-spline). 처음과 끝점을 통과하도록 만들기 위해서는 knot 벡터의 시작 $(p+1)$개 성분이 같은 값을 갖고, 마지막 $(p+1)$개 성분도 같은 값을 갖도록 조정하면 된다(clamped B-spline):

$$clamped: u[0]=u[1]=...=u[p],...,u[n+1]=...=u[n+p]=u[n+p+1]$$

knot는 균일할 필요는 없지만, 균일한 경우는 보통

$$ u_i = \left\{ \begin{array} {rcl} 0 & , & 0 \le i \le p, \\ \frac{i-p}{n+1-p}&, & p+1\le i \le n \\ 1&,& n+1\le i \le n+p+1\end{array}\right.$$

로 선택한다. 

ref: ae.sharif.edu/~aerocad/curve%20modelling-B_Spline.pdf

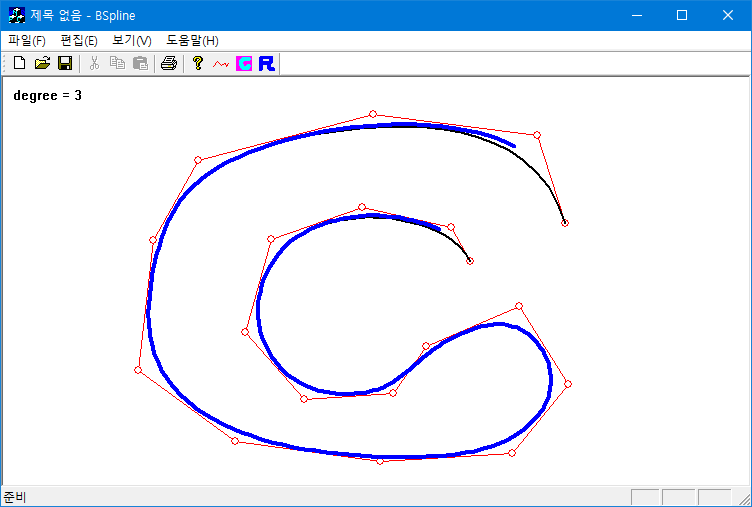
clamped(black), open(blue)

// Note, p = degree;
void BSpline(int p, std::vector<CPoint>& control, int resolution, CDC *pDC) {
    int n = control.size() - 1;  ASSERT(n > 0);
    std::vector<double> u(n + p + 2);                // knot vector;
    calculateKnots(&u[0], n, p);                     // uniform knot;
    double delta = (u[n + p + 1] - u[0]) / (resolution - 1);  // parameter increment;
    CPoint Q;
    for (double t = u[0] ; t <= u[n+p+1]; t += delta) {
        calculatePoint(&u[0], n, p, t, &control[0], &Q);
        if (i == 0) pDC->MoveTo(Q);
        pDC->LineTo(Q);
    }
    pDC->LineTo(control[n]);
}
// de Boor Cox's algorithm;
double Blend(int i, int p, double *u, double t) {  
    if (p == 0) { // termination condition of recursion;
        if ((u[i] <= t) && (t < u[i+1]))        return 1;
        else                                    return 0;
    }
    else {
        double coef1, coef2;
        if (u[i+p] == u[i]) {
            if (t == u[i])  coef1 = 1;
            else            coef1 = 0;
        } 
        else                coef1 = (t - u[i]) / (u[i+p] - u[i]); 
        
        if (u[i+p+1] == u[i+1]) {
           if (t == u[i+1]) coef2 = 1;
           else             coef2 = 0;
        } 
        else                coef2 = (u[i+p+1] - t) / (u[i+p+1] - u[i+1]);
        return coef1 * Blend(i, p-1, u, t) + coef2 * Blend(i+1, p-1, u, t);
    }
}
// clamped b-spline knot vector; uniform example;
// u[0]=u[1]= ... =u[p],.....,u=[n+p-2]=u[n+p-1]=u[n+p]=u[n+p+1]
void calculateKnots(double *u, int n, int p) {
    int j = 0; 
    while (j <= p)     u[j++] = 0;                 // multiplicity = p+1;
    while (j <= n)     u[j++] = j - p;             // m = n+p+1;
    while (j <= n+p+1) u[j++] = n - p + 1;         // multiplicity = p+1;
}
void calculatePoint(double *u, int n, int p, double t, CPoint *control, CPoint *output) {
    double x = 0, y = 0;
    for (int i = 0; i <= n; i++) {
        double b = Blend(i, p, u, t);
        x += control[i].x * b;
        y += control[i].y * b;
    }
    output->x = int(x + 0.5);
    output->y = int(y + 0.5);
}