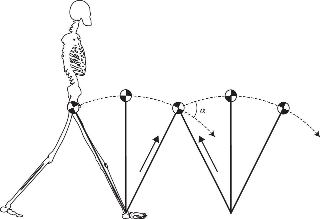
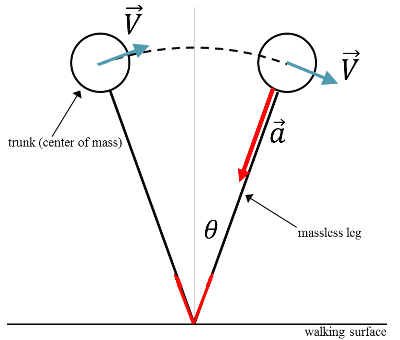
진자의 주기를 구할 때 보통 작은 진동 근사를 사용한다. 진자의 진폭이 크지 않는 경우 주기는 진폭에 무관하게 일정한 값 $T_0=2\pi \sqrt {\frac {\ell}{g}}$를 갖는다. 그럼 진폭이 커지는 경우는 어떻게 될까?

운동 방정식을 써도 되지만 역학적 에너지가 보존되므로 이를 이용하면(회전 관성: $I=m\ell^2$, 진폭=$\theta_0$)
$$ \frac {1}{2} I \Big(\frac {d\theta}{dt}\Big)^2 + mg \ell (1 - \cos\theta)=\text{const}= mg\ell (1- \cos \theta_0) \\ \rightarrow \quad \Big(\frac {d\theta}{dt} \Big)^2 =\frac {2g}{\ell} (\cos \theta- \cos \theta_0).$$
우변을 $\theta_0, ~\theta$에 대해서 전개하면
$$ \Big( \frac { d\theta}{dt } \Big)^2 = \frac {g}{\ell}\Big(\theta_0^2 -\frac {1}{12} \theta_0^4 - \theta^2 + \frac {1}{12} \theta^4+...\Big) =\frac{g}{\ell}(\theta_0^2 -\theta^2) \Big( 1 - \frac{1}{12} (\theta_0^2 + \theta^2)+...\Big)$$로 써지는데 작은 각 근사를 벗어났을 때 가장 큰 기여를 하는 $-(\theta_0^2 + \theta^2 ) /12$항이 음의 기여를 한다. 이는 같은 위치에서 작은 각 근사를 할 때보다 각속도가 더 작아짐을 의미한다. 따라서 진자가 더 느리게 움직여서 주기가 길어질 것이라는 예측을 구체적인 계산 없이도 할 수 있게 된다.
이제 주기를 구해보자. 에너지 보존식에서 변수 분리를 해서 적분하면 주기에 대한 식
$$T = \int dt = 4 \sqrt {\frac {\ell}{2g}} \int_0^{\theta_0} {\frac {d\theta}{\sqrt {\cos \theta - \cos \theta_0}}}$$을 얻는다. 여기서 $\sin(\theta/2) = \sin (\theta_0/2) \sin(\varphi )$로 치환을 하면
$$T = 4\sqrt { \frac { \ell }{g}} \int_0^{\pi/2} {\frac {d \varphi}{\sqrt {1 - k^2 \sin^2 \varphi}}}, \quad k^2 = \sin^2(\theta_0/2).$$
진폭이 작은 경우($\theta_0 \ll 1 ~\Rightarrow ~k\rightarrow 0)$는 적분 값이 $\frac {\pi}{2}$이므로 $T \rightarrow 2\pi \sqrt {\frac {\ell}{g} }$가 됨을 확인할 수 있다. 위 적분은 타원 적분이라고 부르고 $k$가 주어지면 수치 연산을 통해서 그 값을 얻을 수 있다.
좀 더 직관적으로 진폭에 따른 주기의 변화를 보기 위해서 (진자의 경우 $k^2 \le \frac {1}{2}$이므로) 급수 전개를 하면,
$$\frac {1}{\sqrt {1-k^2 \sin^2\varphi}} = 1 +\frac {1}{2} k^2\sin^2 \varphi +\frac {1}{2}\frac {3}{2} k^4 \sin^4 \varphi +\dots $$
이므로 주기는
$$T = 2\pi \sqrt { \frac {\ell}{g} } \left [ 1 + \Big( \frac {1}{2} \Big)^2 k^2 + \Big( \frac {1}{2} \frac {3}{4} \Big)^2 k^4 + \dots \right]\qquad \left( k = \sin \frac{\theta_0}{2} \right)$$
로 표현된다. 이 식은 진자의 진폭($\theta_0$)이 커지면 주기도 길어진다는 것을 명확히 보여준다.

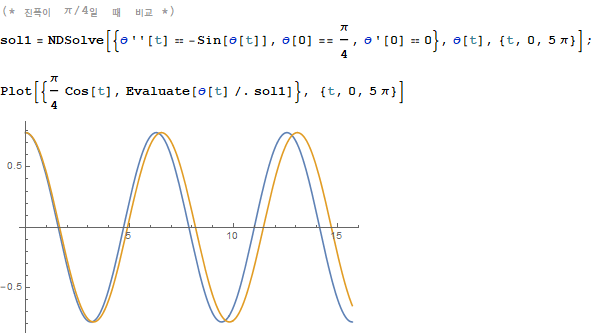
강의동영상을 볼 수 있는 곳:
'Physics > 역학' 카테고리의 다른 글
| 바닥에 먼저 닿는 물체는? (0) | 2021.01.21 |
|---|---|
| 마찰력은 도움이 될까? (0) | 2021.01.21 |
| 물이 새는 두레박이 달린 진자의 주기는 (0) | 2021.01.17 |
| 왜 공은 움직이지 않을까? (0) | 2021.01.17 |
| 두레박이 달린 진자 (0) | 2021.01.17 |