단위구 내부점 사이의 평균 거리(mean distance between 2 points in a ball)

단위구 내의 두 지점을 $\vec{r}_1$, $\vec{r}_2$라면 두 지점이 선택될 확률이 

$$ P(\vec{r}_1, \vec{r}_2) = \frac{dr_1^3}{B_1}\times \frac{dr_2^3}{B_1}, ~~~~B_1=\text{volume of unit ball} = \frac{4\pi}{3}$$이므로 두 지점의 사이거리의 평균은

$$ \left< |\vec{r}_1 - \vec{r}_2| \right> =\frac{1}{B_1^2} \iint_\text{unit ball} |\vec{r}_1 - \vec{r}_2|   {dr_1^3 dr_2^3} $$

$ \vec{r}_1$과 $\vec{r_2}$의 사이각이 $\theta$일 때 고정된 $\vec{r}_1$에 대해서 $\vec{r}_2$의 극좌표 고도각으로 선택하면 $r_2$에 대한 적분은

$$ I_2 = \int_\text{unit ball} | \vec{r}_1 - \vec{r}_2| dr_2^3$$

$$= 2\pi \int_{0}^1 r_2^2 dr_2 \int_{-1}^1 d \cos \theta \sqrt{r_1^2 + r_2^2 - 2r_1 r_2 \cos \theta }  $$

$$= \frac{2\pi}{3} \int_0^{1} r_2^2 dr_2 \frac{(r_1 + r_2)^3 -| r_1 - r_2|^3 }{r_1 r_2 } $$

$$= \pi \left(1 + \frac{2}{3} r_1^2 - \frac{r_1^4}{15}\right)$$

따라서 사이거리의 평균은

$$ \left< |\vec{r}_1 - \vec{r}_2|\right>= \frac{4 \pi}{B_1^2 } \int_0^1 r_1^2 dr_1 \pi \left(1 + \frac{2}{3} r_1^2 - \frac{r_1^4}{15}\right)$$

$$ = \frac{1}{B_1^2} \frac{64 \pi^2}{ 35} = \frac{36}{35}$$

이전 포스팅에서 거리 역수의 평균이 $\frac{6}{5}$임을 보였는데, 평균거리가 이 값의 역수로 주어지지는 않는 점이 의외다.

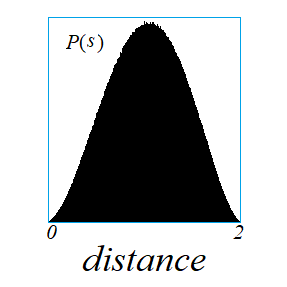
아래 그림은 거리에 대한 확률밀도함수를 Monte Carlo 시뮬레이션으로 구한 결과이다. 실제로 거리에 따른 확률밀도함수를 임의의 차원에서 구할 수 있는데, 3차원의 단위구는(ref: J. Math. Phys., Vol. 41, No. 4, April 2000, https://kipl.tistory.com/733)

$$ P_3(s) = \frac{3}{16} s^2 (2-s)^2(4+s),~~~~0\le s\le 2$$

로 계산이 된다. 이 확률밀도함수의 최대값은 $s=1$이 아니라 $s=\frac{1}{5}\sqrt{105}-1=1.04939$ 에서 나온다. $P_3(s)$를 이용하면$$ <s>= \int_0^2 P_3(s) s ds = \frac{36}{35}$$를 얻고, 거리의 역수의 평균은$$ <\frac{1}{s}> = \int_0^2 P_3(s) \frac{1}{s} ds = \frac{6}{5}$$도 얻을 수 있다. 

#define TWO_PI 6.28318530717958647692
// picking a random vector inside an unit ball;
void randomVector(double &x, double &y, double &z) {
    double a = double(rand()) / RAND_MAX;		//[0,1] = radius;
    double b = double(rand()) / RAND_MAX * 2 - 1; //[-1,1] = cos(theta);
    double c = double(rand()) / RAND_MAX * TWO_PI; //[0, 2PI] = azimuthal; 
    a = pow(a, 1.0 / 3.0);
    x = a * sqrt(1 - b * b) * cos(c);
    y = a * sqrt(1 - b * b) * sin(c);
    z = a * b;
}
// Calculate the distance between two randowm points selected 
// inside an unit ball;
double randomDistance() {
    double x1, y1, z1, x2, y2, z2;
    randomVector(x1, y1, z1);
    randomVector(x2, y2, z2);
    x1 -= x2;
    y1 -= y2;
    z1 -= z2;
    return sqrt(x1 * x1 + y1 * y1 + z1 * z1);
}
void meanDistSphere(CRaster& raster) {
    double R = 100;
    int trials = 5000000;
    srand(unsigned(time(NULL)));
    std::vector<int> hist(2 * int(R + .5) + 1, 0);
    for (int i = trials; i-->0;) {
        double d = R * randomDistance();
        hist[int(d)]++;
    }
    double s = 0, sx = 0, sxx = 0;
    double maxh = 0;
    for (int i = hist.size(); i--> 0; ) {
        double h = hist[i];
        maxh = max(h, maxh);
        s += h;
        sx += h * i;
        sxx += h * i * i;
    }
    double mean = sx / s;
    double var = (sxx - sx / s) / s;
    double sdev = sqrt(var);
    // CRaster raster;
    raster.SetDimensions(hist.size(), hist.size(), 24);
    CSize sz = raster.GetSize();
    memset(raster.GetDataPtr(), 0xFF, raster.GetDataSize());
    for (int x = sz.cx; x--> 0; ) {
        int h = int(double(sz.cy) * hist[x] / maxh);
        for (int y = h; y--> 0; ) 
            raster.SetPixel(x, sz.cy-1-y, 0);
    }
    // SaveRaster(raster, "hist.bmp");
}