단위원 내부점 사이의 평균 거리(mean distance between two points in a circular disk)

단위원에서 선택한 임의의 두 지점의 사이거리 $s$가 $0\le s\le 2$이 확률밀도함수는 

$$ P(s) =\frac{1}{D_1^2}\iint _\text{unit disk} d^2r d^2 r' \delta (|\vec{r} - \vec{r}'|-s) ,~~~~D_1 = \pi $$

먼저

$$ L(\vec{r}, s) = \int_\text{unit disk} d^2r' \delta (|\vec{r}'-\vec{r}|-s) $$

은 델타함수 제한조건 때문에 $\vec{r}$을 중심으로 한 반지름 $s$인 원과 단위원의 겹치는 영역의 경계의 길이를 의미함을 알 수 있다. 이 $L(\vec{r},s)$가 구해지면 $P(s)$는 이 값을 단위원에 대해 적분을 하면 되는데, 그 값은 단위원의 중심엣 $\vec{r}$가 거리에만 의존함을 쉽게 알 수 있다. 따라서 $\vec{r}$가, 예를 들면  $x$축 위에 있는 경우만 고려하면 충분하다. 또, $L(\vec{r},s) = L(|\vec{r}|=r, s)$이므로

$$\int_\text{unit disk} d^2r L(r,s ) = 2\pi \int_0^1 r dr L(r, s)$$

이제 $\vec{x}$을 중심으로 한 반지름 $s$인 원이 완전히 단위원에 포함이 되는 경우는 원과 단위원의 겹치는 영역이 반지름 $s$인 원이므로 

$$  r + s < 1~~\to ~~~L(r, s)=  2\pi s$$

이고, 원호 일부가 단위원 밖으로 나가는 경우는 두 가지 경우(그림의 $\theta$가 예각 또는 둔각)를 생각할 수 있는데,

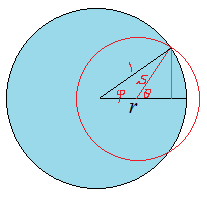
두 경우 모두 단위원과 겹치는 영역의 원호의 길이는 그림에서 $2(\pi - \theta)s$인데, $$\sin \varphi = s \sin \theta,~~~~\cos \varphi - s \cos \theta = r$$

$$\to~~~ \cos \theta = \frac{1-r^2 -s^2 }{2rs}$$

$$ r+s>1~~\to~~ L(r, s) = 2(\pi - \theta)s =  2s\left( \pi - \cos ^{-1} \frac{1- r^2 - s^2 }{2rs}\right) $$

로 표현된다. 따라서 사이거리에 대한 확률밀돟함수는

$$P(s) = \frac{2\pi}{\pi^2} \int_0^1 rdr L(r, s) $$$$= 4s \int_0^{1-s} r dr + \frac{4s}{\pi} \int_{1-s}^1 rdr \left( \pi - \cos^{-1} \frac{1- r^2 - s^2 }{2rs} \right)$$

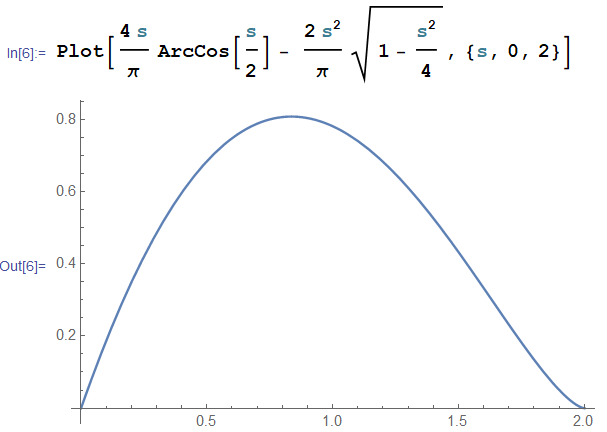
$$=\frac{4s}{\pi} \cos^{-1} \frac{s}{2} - \frac{2s^2}{\pi} \sqrt{ 1 -\frac{s^2}{4}} $$

이 분포를 이용하면 단위원 내부에서 선택된 두 점간의 평균거리는

$$  \left< |\vec{r}-\vec{r}'| \right>= \int_0^2 P(s)s ds = \frac{128}{45\pi} = 0.9054$$

$$  \left< |\vec{r}-\vec{r}'|^2 \right>= \int_0^2 P(s)s^2 ds = 1$$

$$  \left< \frac{1}{|\vec{r}-\vec{r}'|} \right>= \int_0^2 P(s)\frac{1}{s} ds = \frac{16}{3\pi}$$