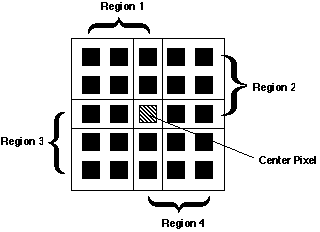
Kuwahara filter는 주어진 픽셀을 한 코너로 하는 4개 block 중에서 분산이 가장 작은 블록의 평균으로 중앙 픽셀 값을 대체하는 비선형 filter다. 이 필터를 적용하면 균일한 영역에서 spike noise 픽셀은 주변의 영역의 픽셀 값으로 대체되므로 제거될 수 있고, edge 라인을 기준으로 수직방향으로는 거의 균일한 영역이므로 필터링을 하더라도 edge가 뭉개지지 않음을 알 수 있다. Kuwahara filter는 이미지의 노이즈를 제거하고 edge를(위치) 보존하는 특성을 가진다. 윈도의 크기가 5x5인 경우 4개의 3x3영역에서 평균과 분산을 계산해서 중앙 픽셀의 값을 결정한다. integral 이미지를 사용하면 block의 평균과 분산을 매번 새롭게 계산할 필요가 없으므로 연산 비용이 많이 감소한다.


Kuwahara filter보다 더 향상된 filter로는 symmetric nearest neighbour (SNN) filter가 있다. 이 filter는 기준 픽셀에서 대칭 지점에 있는 두 지점의 픽셀 값 중에서 중앙 픽셀 값에 가까운 것을 취해서 평균값을 취한다.
아래 코드는 gray 이미지에 대해 Kuwahara filter을 구현한 것으로 컬러 이미지의 경우는 RGB 채널별로 따로 적용하면 된다. 그리고 경계 영역에서는 처리를 하지 않도록 만들었다.
#define GET_SUM(x,y) sum[(y)*width+(x)]
#define GET_SUM2(x,y) sum2[(y)*width+(x)]
#define BLK_SUM(x,y) ((GET_SUM((x),(y)) + GET_SUM((x)-hs1,(y)-hs1) \
- GET_SUM((x)-hs1,(y)) - GET_SUM((x),(y)-hs1)))
#define BLK_SUM2(x,y) ((GET_SUM2((x),(y)) + GET_SUM2((x)-hs1,(y)-hs1) \
- GET_SUM2((x)-hs1,(y)) - GET_SUM2((x),(y)-hs1)))
void integral_image(BYTE *image, int width, int height, int *sum);
void integral_image_sq(BYTE *image, int width, int height, int *sum2);
// output -> input;
void kuwahara_filter (std::vector<BYTE> &image, int width, int height, int size)
{
// integral image; for window mean;
std::vector<int> sum(width * height, 0);
// integral image of square; for window variance;
stt::vector<int> sum2(width * height, 0);
for (int y = 0, yw = 0; y < height; y++, yw += width ) {
int s = 0, ss = 0;
for (int x = 0; x < width; x++ ) {
int a = image[yw + x];
s += a; ss += a * a;
sum[yw + x] = s;
sum2[yw + x] = ss;
}
}
for (int x = 0; x < width; x++ )
for (int y = 1, yw = width; y < height; y++, yw += width ) {
sum[yw + x] += sum[yw - width + x];
sum2[yw + x] += sum2[yw - width + x];
}
// do filtering;
size = ((size >> 1) << 1) + 1; // make window size be an odd number;
const int offset = ( size - 1 ) >> 1;
const int hs1 = ( size + 1 ) >> 1;
const int nn = hs1 * hs1; // # of pixels within the window;
const int dx[] = {0, offset, 0, offset};
const int dy[] = {0, 0, offset, offset};
int var[4], mean[4];
for (int y = height - hs1; y-->hs1;)
for (int x = width - hs1; x-->hs1;) {
int vmin = INT_MAX, winner = 0;
for (int k = 0; k < 4; ++k) {
mean[k] = BLK_SUM(x+dx[k], y+dy[k])/nn;
var[k] = BLK_SUM2(x+dx[k], y+dy[k])/nn - mean[k]*mean[k];
if (vmin > var[k])
vmin = var[k], winner = k;
}
int a = mean[winner];
image[y*width + x] = a > 255 ? 255 : a < 0 ? 0 : a;
}
};728x90
'Image Recognition' 카테고리의 다른 글
| Union-Find 알고리즘을 이용한 영역분할 (0) | 2021.01.11 |
|---|---|
| Multilevel Otsu Thresholding (0) | 2021.01.09 |
| Moving Average을 이용한 Thresholding (0) | 2020.11.26 |
| Expectation Maximization Algorithm for Two-Component Gaussian Mixture (0) | 2017.01.02 |
| Union-Find Connected Component Labeling (0) | 2012.11.01 |




