Geometry & Recognition

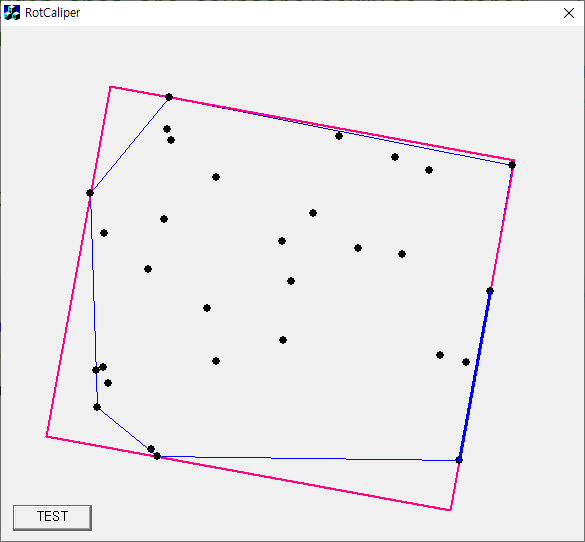
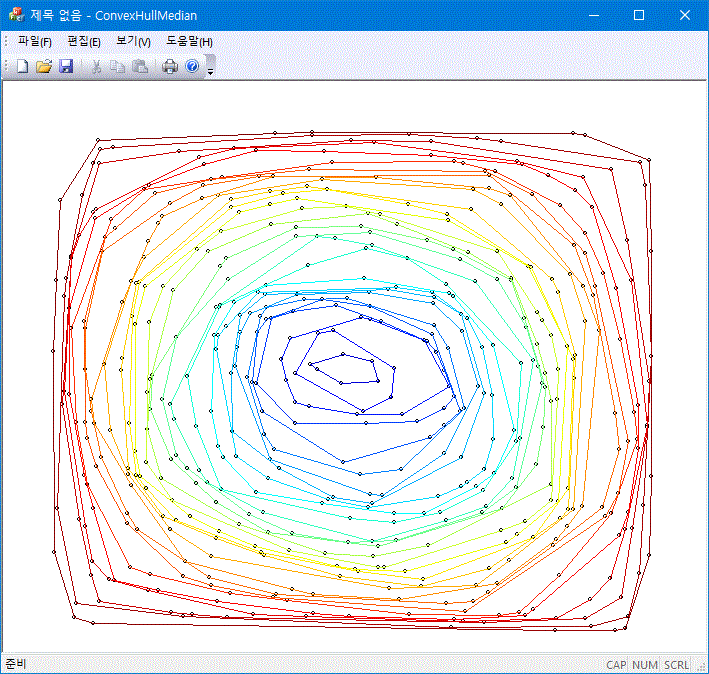
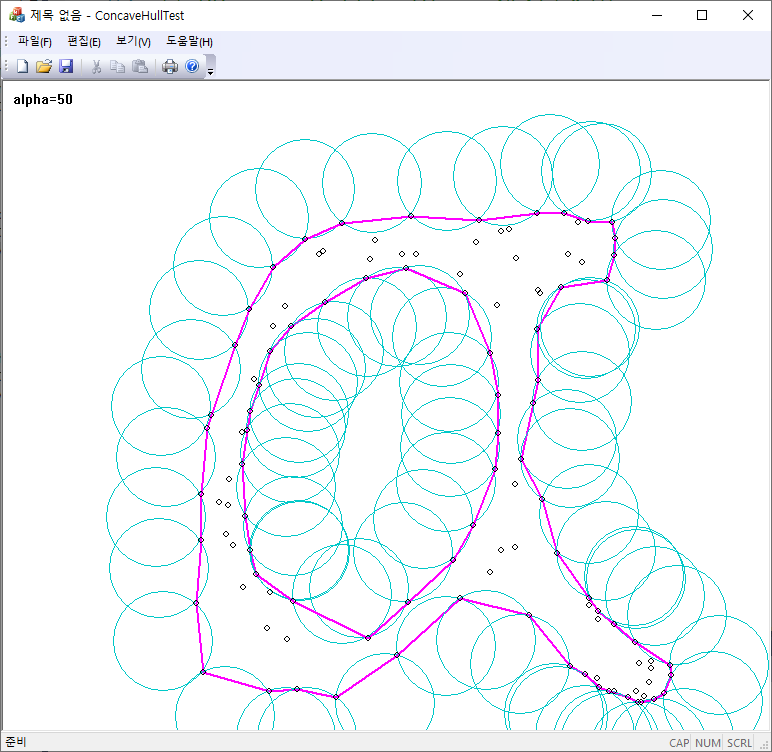
In computational geometry, an alpha shape, or α-shape, is a family of piecewise linear simple curves in the Euclidean plane associated with the shape of a finite set of points. https://en.wikipedia.org/wiki/Alpha_shape

class AlphaShape {
    double alpha;
    std::set<std::pair<int,int>> Border; //pair;
public:
    AlphaShape() { }
    AlphaShape(CDC *pDC, std::vector<CfPt>& Q, const double radius = 50) {
        if (Q.size() < 2) return;
        alpha = radius;
        const double alphaSq = alpha * alpha;
        const double diameter = 2 * alpha;
        for (int i = 0; i < Q.size(); ++i) {
            const CfPt &p = Q[i];
            for (int j = 0; j < i; ++j) {
                const CfPt &q = Q[j];
                if (q == p) continue;
                const double edist = p.Dist(q); 
                // 두 점의 사잇거리가 지름보다 크면 edge가 안됨;
                if (edist > diameter) continue;                     

                // 두 점을 원주에 포함하는 반지름 alpha인 두 원을 찾음;
                // note that c1 == c2 if edist == diameter;
                double scale = sqrt(alphaSq - (edist/2)*(edist/2));
                CfPt n = (q - p) * scale / edist;
                CfPt mid = (q + p) / 2;
                CfPt c1 = mid + n.Rot90(); // CfPt(mid.x - ny, mid.y + nx);
                CfPt c2 = mid - n.Rot90(); // CfPt(mid.x + ny, mid.y - nx);

                // alpha shape의 변이 되기 위해서는 두 원 중 하나는
                // 다른 점들을 포함하지 않아야 함;
                bool c1_empty = true, c2_empty = true;
                for (int k = Q.size(); (k-->0) && (c1_empty || c2_empty);) {
                    if (Q[k] == p|| Q[k]== q) continue; //i==k || j==k?
                    if (c1.DistSq(Q[k]) < alphaSq) c1_empty = false;
                    if (c2.DistSq(Q[k]) < alphaSq) c2_empty = false;            
                }

                if (c1_empty || c2_empty) {                  
                    if (c1_empty) drawCircle(pDC, c1);
                    if (c2_empty) drawCircle(pDC, c2);
                    // draw edge;
                    drawEdge(pDC, p, q);
                    //Border.insert(std::make_pair(i,j));
                }
            }
        }
    } 
    void drawEdge(CDC *pDC, const CfPt &p, const CfPt &q) {
        CPen pen(PS_SOLID,2,RGB(255,0,255)); //magenta;
        CPen *pOld = pDC->SelectObject(&pen);
        pDC->MoveTo(p); pDC->LineTo(q);
        pDC->SelectObject(pOld);
    }
    void drawCircle(CDC *pDC, const CfPt &c) {
        CPen pen(PS_SOLID, 1, RGB(0,200,200));
        CPen *pOld = pDC->SelectObject(&pen);
        pDC->SelectObject(GetStockObject(NULL_BRUSH));
        pDC->Ellipse(c.x-alpha, c.y-alpha, c.x+alpha, c.y+alpha);
        pDC->SelectObject(pOld);		
    }
    std::set<std::pair<int,int>> getBorder() {
        return Border;
    }
};

주어진 점집합의 Convex hull을 찾는 알고리즘은 보통 $n \log(n)$ 정도의 time complexity를 가지고 있다. 그러나 점집합의 사이즈가 매우 커지는 경우에는 degeneracy로 인해 optimal한 알고리즘을 사용할 때 매우 주의를 기울려야 한다. 영상처리에서 convex hull을 사용할 때 근사적인 알고리즘만 있어도 충분한 경우가 많이 있는데 이런 경우에 이용할 수 있도록 알고리즘을 수정하자. Convex hull을 만들기 위해서는 점집한을 일정한 순서로 정렬을 하는 과정이 있는데 이 과정이 알고리즘의 가장 복잡한 부분이기도 하다. 이 정렬 과정을 근사적으로 수행하기 위해서 점집합을 수평(또는 수직)으로 일정한 간격으로 나누어진 구간으로 분류를 하자. 이 과정은 주어진 점집합을 한 번 순환만 하면 완료된다. 그런 다음 각 구간에서 수직방향으로(처음 수직방향으로 구간을 나누었으면 수평방향) 가장 바깥에 있는 두 점을 그 구간의 대표점으로 잡아 convex hull을 구하면 원 집합의 근사적인 convex hull이 된다. 이 구간 대표점들은 이미 정렬이 되어 있으므로 대표점 수(~구간 수)에 비례하는 시간 복잡도 이내에 알고리즘이 수행된다. 그리고 구간의 수를 점점 늘릴수록 정확한 convex hull에 근접하게 된다.  아래 그림은 500,000개 점의 근사적인 convex hull을 보여준다(bins=128)

// cross(P1-P0, P2-P0);
// = := colinear;
// < := <p0,p1,p2> CW order;
// > := <p0,p1,p2> CCW order;
static
int ccw(const CPoint &P0, const CPoint &P1, const CPoint &P2 ) {
    return (P1.x - P0.x)*(P2.y - P0.y) - (P2.x - P0.x)*(P1.y - P0.y);
}
std::vector<CPoint> approximateHull(const std::vector<CPoint>& Q, int bins) {
    if (Q.size() < 3) return std::vector<CPoint> ();
    if (bins < 0) bins = max(1, Q.size()/10);
    int Lmin = 0, Lmax = 0, Rmin = 0, Rmax = 0;
    int left = Q[0].x, right = left;
    for (int i = 1; i < Q.size(); i++) {
        if (Q[i].x <= left) {
            if (Q[i].x < left) {
                Lmin = Lmax = i;
                left = Q[i].x;
            } 
            else 
                if (Q[i].y < Q[Lmin].y) Lmin = i;
                else if (Q[i].y > Q[Lmax].y) Lmax = i;
        }
        if (Q[i].x >= right) {
            if (Q[i].x > right) {
                Rmin = Rmax = i;
                right = Q[i].x;
            }
            else 
                if (Q[i].y < Q[Rmin].y) Rmin = i;
                else if (Q[i].y > Q[Rmax].y) Rmax = i;
        }
    }
    if (left == right) return std::vector<CPoint> (); //vertical line;
    //
    std::vector<int> slotYhigh(bins + 2, -1);
    std::vector<int> slotYlow(bins + 2, -1);
    slotYlow.front() = Lmin; 
    slotYhigh.front() = Lmax;
    slotYlow.back()  = Rmin;
    slotYhigh.back()  = Rmax;
    //
    const CPoint &A = Q[Lmin];
    const CPoint &B = Q[Rmin];
    const CPoint &C = Q[Lmax];
    const CPoint &D = Q[Rmax];
    for (int i = 0; i < Q.size(); i++) {
        if (Q[i].x == right || Q[i].x == left) continue;
        if (ccw(A, B, Q[i]) < 0) { // below line(A,B);
            int b = 1 + (bins * (Q[i].x - left)) / (right - left);
            if (slotYlow[b]==-1) slotYlow[b] = i;
            else if (Q[i].y < Q[slotYlow[b]].y) slotYlow[b] = i;
            continue ;
        }
        if (ccw(C, D, Q[i]) > 0) {// above line(C,D);
            int b = 1 + (bins * (Q[i].x - left)) / (right - left);
            if (slotYhigh[b]==-1) slotYhigh[b] = i;
            else if (Q[i].y > Q[slotYhigh[b]].y) slotYhigh[b] = i;
            continue;
        }
    }
    std::vector<CPoint> hull(Q.size());
    int s = -1;
    for (int i = 0; i <= bins + 1; i++) {
        if (slotYlow[i]==-1) continue;
        while (s > 0) 
            if (ccw(hull[s-1], hull[s], Q[slotYlow[i]]) > 0) break;
            else s--;
        
        hull[++s] = Q[slotYlow[i]];
    };
    if (Rmax != Rmin) hull[++s] = Q[Rmax];
    //
    int s0 = s ;
    for (int i = bins; i >= 0; i--) {
        if (slotYhigh[i]==-1) continue;
        while (s > s0) 
            if (ccw(hull[s-1], hull[s], Q[slotYhigh[i]]) > 0) break;
            else s--;
        
        hull[++s] = Q[slotYhigh[i]];
    }
    if (hull[s] == hull[0]) s--;
    hull.resize(s+1);
    return hull;
}

주어진 점들을 감싸는 최소  면적의 직사각형은 먼저 convex hull을 구한 후 rotating caliper을 써서 구할 수 있다. 다음 코드는 반시계방향으로 정렬된 convex hull을 이용해서 minimum volume box을 구한다. 처음 좌표축 방향으로 정렬된 bounding box을 이용해서 가장 작은 각을 형성하는 convex hull의 한 변을 찾고, 그 변으로 만들어지는 bounding box를 구한다. 반시계방향으로 bounding box가 convex hull의 변을 순차적으로 접하도록 회전시키면서 최소 면적인 경우를 찾으면 된다. 이는 convex hull을 바닥에서 굴리면서 bounding box을 찾는 경우로 생각해 보면 더 쉽다. bounding box가 convex hull의 모든 변을 다 순회하면 알고리즘이 종료되므로  time complexity는 $O(N)$이다.

void MinVolumeBox(const std::vector<CfPt>& chull, CfPt mvbox[4]) {
    if (chull.size() < 3) return;
    std::vector<CfPt> edges(chull.size());
    std::vector<int>  visited(chull.size(), 0);  // initialized = 0;
    enum {BB_NONE, BB_LEFT, BB_RIGHT, BB_BOTTOM, BB_TOP};
    for (int i = 0; i < chull.size(); i++) {
        const CfPt e = chull[(i+1) % chull.size()] - chull[i];
        edges[i] = e / e.Norm();// make a unit vector;
    }
    // 먼저 좌표의 최소-최대 값을 구한다;
    // index을 순환할 때, 항상 최대-최소가 (index+chull.size)%chull.size가 되게
    double xmin = chull[0].x, xmax = xmin;
    double ymin = chull[0].y, ymax = curr;
    int left = 0, bot = 0, right = 0, top = 0 ;
    for (int i = 1; i < chull.size(); i++) {
        if (chull[i].x <= xmin)      { xmin = chull[i].x; left = i;}
        else if (chull[i].x >= xmax) { xmax = chull[i].x; right = i;}
        if (chull[i].y <= ymin)      { ymin = chull[i].y; bot = i;}
        else if (chull[i].y >= ymax) { ymax = chull[i].y; top = i;}
    }
    if (chull[0].x <= xmin)       { xmin = chull[0].x; left = 0;}
    else if ( chull[0].x >= xmax) { xmax = chull[0].x; right = 0;}
    if (chull[0].y <= ymin)       { ymin = chull[0].y; bot = 0;}
    else if (chull[0].y >= ymax)  { ymax = chull[0].y; top = 0;}

    /*____Initial mvbox Setting____*/
    CfPt center = CfPt(xmin + xmax, ymin + ymax)/2;
    CfPt ax0 = CfPt(1,0), ax1 = CfPt(0,1);	// mvbox의 unit vectors;
    CfPt eh = ax0, ev = ax1;				// working unit vectors;
    double hscale  = (xmax - xmin) / 2; 
    double vscale  = (ymax - ymin) / 2;
    double minarea = hscale * vscale;		// area / 4;
    int done = 0;
    while (!done) {
        // edges[bot]는 chull[bot+1]-chull[bot];
        // edges[bot],edges[right],edges[top],edges[left] 중에서
        // 현재의 mvbox의 변(eh, ev,-eh,-ev)과 가장 작은 각(max_cosine)을 이루는 
        // edge를 찾음;
        int iflag = BB_NONE;
        double	max_cosine = 0;
        double	cosine = eh * edges[bot];
        if (cosine > max_cosine) { max_cosine = cosine; iflag = BB_BOTTOM;}

        cosine = ev * edges[right]; ;
        if (cosine > max_cosine) { max_cosine = cosine; iflag = BB_RIGHT;}
        
        cosine = -eh * edges[top]; 
        if (cosine > max_cosine) { max_cosine = cosine; iflag = BB_TOP;}
        
        cosine = -ev * edges[left]; 
        if (cosine > max_cosine) { max_cosine = cosine; iflag = BB_LEFT;}
        
        switch (iflag) {
        case BB_BOTTOM:
            if (!visited[bot]) {// edges[bot]가 mvbox의 한변에 포함됨;
                eh = edges[bot]; ev = eh.Rot90(); 
                // 다음 변으로 회전;
                visited[bot] = 1;
                if (++bot == chull.size()) bot = 0;
            } else done = 1;
            break;
        case BB_RIGHT:
            if (!visited[right]) {// edges[right]가 mvbox의 한변에 포함됨;
                ev = edges[right]; eh = -ev.Rot90(); 
                // 다음 변으로 회전;
                visited[right] = 1;
                if (++right == chull.size()) right = 0;
            } else done = 1;
            break;
        case BB_TOP:
            if (!visited[top]) { // edges[top]이 mvbox의 한변에 포함됨;
                eh = -edges[top]; ev = eh.Rot90(); 
                // 다음 변으로 회전;
                visited[top] = 1;
                if (++top == chull.size()) top = 0;
            } else done = 1;
            break;
        case BB_LEFT:
            if (!visited[left]) {// edges[left]가 mvbox의 한변에 포함됨;
                ev = -edges[left]; eh = -ev.Rot90(); 
                // 다음 변으로 회전;
                visited[left] = 1;
                if (++left == chull.size()) left = 0;
            } else done = 1;
            break;
        case BB_NONE: // polygon이 직사각형임;
            done = 1;
            break;
        }
        // check area of mvbox;
        double len0 = eh * (chull[right] - chull[left]) / 2;
        double len1 = ev * (chull[top] - chull[bot]) / 2;
        double area = len0 * len1; //면적의 1/4 임;
        if (area < minarea) {
            minarea	= area;
            ax0	= eh; ax1 = ev;
            hscale = len0; vscale = len1;
            // box center: tt = left 기준 top-bot을 연결하는 vector/2;
            CfPt tt = (chull[top] + chull[bot]) / 2 - chull[left];
            double zz = ev * tt; 
            center = eh * len0 + ev * zz + chull[left];
        }
    }
    eh = ax0 * hscale; // recover original scale;
    ev = ax1 * vscale; // recover original scale;
    mvbox[0] = center + eh + ev;
    mvbox[1] = center - eh + ev;
    mvbox[2] = center - eh - ev;
    mvbox[3] = center + eh - ev;
}

2차원 점집합의 median

• www.cs.princeton.edu/~chazelle/pubs/ConvexLayers.pdf
• arxiv.org/ftp/arxiv/papers/1803/1803.04964.pdf

Convex hull을 찾을 때, 중복점과 일직선상 위에 있는 점들에 대해서 적절한 처리를 하지 않으면 효율적으로 작성된 알고리즘이라도 정상적으로 동작하지 않을 수 있다. 그림은 Graham Scan 알고리즘을 이용해서 50,000개 점들의 convex hull을 구한 결과다. 각 정렬을 하기 위해서는 pivort point가 필요한데 std::sort()을 호출할 때 compare()에서 global 변수를 쓰지 않기 위해서 첫 원소를 pivot point로 잡아서 사용한다. 정렬 후에는 빼주었던 pivot를 다시 더해준다.

inline int LeftSide(const CPoint &A, const CPoint &B, const CPoint &C) {
    return (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y); // cross(AB, AC);
}
static int cross(const CPoint &p1, const CPoint &p2) {
    return p1.x * p2.y - p1.y * p2.x;
}
static int norm2(const CPoint &p) {
    return p.x * p.x + p.y * p.y;
}
static int compare(const CPoint &a, const CPoint &b) {
    int ccw = cross(b, a);
    // 거리가 먼 곳 --> 가까운 곳;
    if (ccw == 0) return norm2(b) < norm2(a);
    return ccw < 0; // 반시계방향 정렬;
}
static void angularSort(std::vector<CPoint> & pts) {
    if ((pts.size()) < 2) return;
    int id = 0;
    for (int i = pts.size(); i-->0;) 
        if ((pts[id].y > pts[i].y) || (pts[id].y == pts[i].y && pts[i].x > pts[id].x)) 
            id = i;  //lowest--y-value; //largest--x-value;
    std::swap(pts[0], pts[id]);
    for (int i = pts.size(); i-->1;) pts[i] -= pts[0];
    std::sort(pts.begin()+1, pts.end(), compare);
    for (int i = pts.size(); i-->1;) pts[i] += pts[0];
};
// AB와 BC가 나란할 때, AB 방향과 BC방향이 같은가(0) 반대면 (1): dot(AB, BC);
static int folded(const CPoint &A, const CPoint &B, const CPoint &C) {
    return (B.x - A.x) * (C.x - B.x) + (B.y - A.y) * (C.y - B.y) <= 0;
}
std::vector<CPoint> GrahamScan(const std::vector<CPoint>& points) {
    if (points.size() < 3) return std::vector<CPoint> (); //null_vector;
    std::vector<CPoint> pts = points; //clone;
    angularSort(pts);
    std::vector<CPoint> hull(pts.size());
    hull[0] = pts[0];
    int i = 1; 
    while (i < pts.size()) { 
        // peek out points degenerate with pts[0];
        if (pts[i] != hull[0]) {
            hull[1] = pts[i++]; break;  //  (i++)
        }
        i++;
    }
    if (i == pts.size()) return std::vector<CPoint> ();//null_vector;
    int k = 2; // 새로 추가되는 hull index;
    while (i < pts.size()) {
        // (i)가 hull의 left에 있으면(1) hull의 꼭지점에 추가;
        int ccw = LeftSide(hull[k - 2], hull[k - 1], pts[i]); 
        if (ccw > 0) hull[k++] = pts[i++];
        // (i)가 hull의 직전 변과 collinear한 데 반대방향을 향하면 skip;
        else if (ccw == 0 && folded(hull[k - 2], hull[k - 1], pts[i])) ++i;
        // (i)가 hull의 right 또는 위에 있으면(직전 변과 같은 방향)
        // hull의 직전 꼭지점을 순차적으로 제거한 후 다시 검사;
        else --k;
        ASSERT(k >= 2);
    }
    hull.resize(k);
    return hull;
};