Centripetal Catmull-Rom Spline

Spline은 일정한 매개변수 구간 $[a,b]$에서 분포된 값(다차원인 경우는 벡터)을 이용해서 만든 다항식을 의미한다. 매개변수 구간 $[a,b]$는 값이 주어진 부분구간들의 합으로 표현할 수 있는데 이 부분구간의 시작과 끝에 해당하는 매개변수 값을 knot이라고 한다. knot이 매개변수 구간 $[a,b]$에 균일하게 퍼져 있는 경우는 uniform spline, 그렇지 않은 경우는 non-uniform spline이라고 한다.

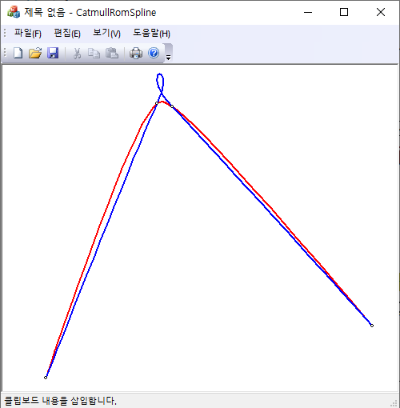
Catmull-Rom spline은 3차 다항식으로 써지는 uniform spline으로 각 knot 위치에서 주어진 값을 통과하므로 interpolation 함수이기도 한다. 그리고 1차 도함수가 연속성을 가지고 있고, knot의 위치 변화나 knot에서 주어진 값의 변화에 곡선이 민감하게 변하지 않는다. 그러나 2차원 이상에는 Catmull-Rom spline이 꼬이는 현상이 발생할 수 있고, 극단적으로는 cusp가 생기는 단점도 가지고 있다.

2차원 이상에서는 Catmull-Rom spline으로 주어진 점(벡터)들을 보간하는 곡선을 찾을 때 uniform이 아니면 knot을 정하는데 모호함이 존재한다. 보통은 순차적으로 주어진 입력점의 직선거리를 이용해서 knot을 정할 수 있는데 이 경우를 chordal Catmull-Rom spline이라고 한다.

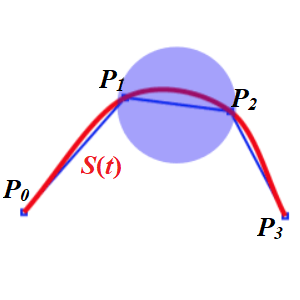
주어진 입력점이 $\{{\mathbf{P}}_0,{\mathbf{P}}_1,{\mathbf{P}}_2,{\mathbf{P}}_3\}$일 때 knot은

$$t_i=t_{i-1}+||{\mathbf{P}}_i–{\mathbf{P}}_{i-1}||$$

더 일반적으로 

$$t_i=t_{i-1}+||{\mathbf{P}}_i-{\mathbf{P}}_{i-1}|{|}^{\alpha },\alpha \in [0,1]$$

로 잡을 수 있는데 이 경우를 centripetal Catmull-Rom spline이라 하며 cusp를 피할 수 있다. 단, 입력점의 중복이 없도록 미리 제거되어야 한다. Spline $\mathbf{S}(t)$는 ${\mathbf{P}}_1$과 ${\mathbf{P}}_2$사이에서

• 3차 함수로 쓰여져야 하고,
• 입력점 통과: $\mathbf{S}(t_1)={\mathbf{P}}_1$, $\mathbf{S}(t_2)={\mathbf{P}}_2$ ,
• 기울기: ${\mathbf{S}}^{\prime }(t_1)=\frac{1}{t_2-t_0}({\mathbf{P}}_2-{\mathbf{P}}_0)$, ${\mathbf{S}}^{\prime }(t_2)=\frac{1}{t_3-t_1}({\mathbf{P}}_3-{\mathbf{P}}_1)$

인 조건을 사용하면 $\mathbf{S}(t)$에 대한 closed form을 얻을 수 있다(참고: 위키피디아). $\mathbf{S}(t)$은 $t_1\le t\le t_2$ 사이에서 정의되고, 곡선을 그릴 때 매개변수를 $t\in [0:1]$ 으로 잡으면 $\mathbf{S}(t)$를 호출할 때는 $t_1+(t_2-t_1)t$를 인자로 사용하면 된다.

ref: http://www.cemyuksel.com/research/catmullrom_param/catmullrom.pdf

https://kipl.tistory.com/226

Catmull-Rom Spline

 

red=centripetal Catmull-Rom Spline

double GetParam(double t, double alpha, const CfPt& p0, const CfPt& p1 ) {
    CfPt p = p1 - p0;
    double dsq = p.x * p.x + p.y * p.y;
	if (dsq == 0) return t;
    return pow(a, alpha / 2) + t;
}
//centripetal catmull-rom spline;
CfPt CRSplineA(double t /*[0:1]*/, 
               const CfPt& p0, 
               const CfPt& p1, 
               const CfPt& p2, 
               const CfPt& p3, double alpha=.5 /*[0:1]*/)
{
    double t0 = 0;
    double t1 = GetParam( t0, alpha, p0, p1 );
    double t2 = GetParam( t1, alpha, p1, p2 );
    double t3 = GetParam( t2, alpha, p2, p3 );
    t = t1 * (1 - t) + t2 * t;
    CfPt A1 = t1==t0 ? p0: p0*(t1-t)/(t1-t0) + p1*(t-t0)/(t1-t0);
    CfPt A2 = t2==t1 ? p1: p1*(t2-t)/(t2-t1) + p2*(t-t1)/(t2-t1);
    CfPt A3 = t3==t2 ? p2: p2*(t3-t)/(t3-t2) + p3*(t-t2)/(t3-t2);
    CfPt B1 = A1 * (t2-t)/(t2-t0) + A2 * (t-t0)/(t2-t0);
    CfPt B2 = A2 * (t3-t)/(t3-t1) + A3 * (t-t1)/(t3-t1);
    return B1 * (t2-t)/(t2-t1) + B2 * (t-t1)/(t2-t1);
}
void DrawCatmullRom(std::vector<CfPt>& Q, CDC *pDC) {  
#define STEPS (20)
    if (Q.size() < 4) return ;
    CPen red(PS_SOLID, 2, RGB(255, 0, 0));
    CPen *pOld = pDC->SelectObject(&red);
    const int n = Q.size();
    // centripetal Catmull-Rom spline;
    for (int i = 0; i < n - 1; i++) {
        pDC->MoveTo(Q[i]);
        // i = 0 인 경우에는 처음 점을 반복, i = n - 2인 경우에는 마지막 점을 반복..
        int ip = max(i - 1, 0);
        int inn = min(i + 2, n - 1);
        for (int it = 1; it <= STEPS; it++)
            pDC->LineTo(CRSplineA(double(it)/STEPS, Q[ip], Q[i], Q[i + 1], Q[inn]));
    };
    pDC->SelectObject(pOld);
    CPen blue(PS_SOLID, 2, RGB(0, 0, 255));
    pOld = pDC->SelectObject(&blue);
    // uniform Catmull-Rom spline;
    for (int i = 0; i < n - 1; i++) {
        pDC->MoveTo(Q[i]);
        // i = 0 인 경우에는 처음 점을 반복, i = n - 2인 경우에는 마지막 점을 반복..
        int ip = max(i - 1, 0);
        int inn = min(i + 2, n - 1);
        for (int it = 1; it <= STEPS; it++)
            pDC->LineTo(CRSpline(double(it)/STEPS, Q[ip], Q[i], Q[i + 1], Q[inn]));
    };
    pDC->SelectObject(pOld);
}