Catmull-Rom Spline

두 개의 점이 주어지는 경우 이들을 잇는 가장 단순한 곡선은 직선이다. 또 직선은 두 점을 잇는 가장 짧은 거리를 갖는 곡선이기도 하다. 그러면 $N$개의 점이 주어지는 경우는 이들 모두 지나는 곡선을 어떻게 찾을까? 구간별로 직선으로 연결을 시켜서 하나의 곡선을 구성할 수 있으나 부드럽게 이어지는 형태의 곡선은 아니다. 곡선이 smooth 함은 그 곡선의 곡률이 잘 정의된다는 의미이다(곡률은 곡선의 이차 미분에 의존한다). 주어진 점들을 연결하는 충분히 짧고 smooth 한 곡선을 찾는 문제는 곡률에 의한 에너지를 최소화시키는 해를 구하는 문제로 환원할 수 있다. 이 문제의 해는 잘 알려진 cubic spline이다. 그러나 cubic spline은 지나는 점(컨트롤 점)의 변동에 대해서 안정적이 아니다. 컨트롤 점 중에서 한 점만 변해도 곡선이 전역적(global)으로 변하는 특성을 나타낸다. 컨트롤 점의 변동이 있을 때 그 점 주위에서만 변화하는 국소 특성을 갖는 곡선을 찾기 위해서는 smoothness 조건을 완화해야 한다. 그렇지만 충분히 부드러운 곡선이어야 하므로 적어도 일차의 미분 값의 연속성 정도는 보장되어야 한다. 이런 특성을 갖는 삼차 곡선이 Catmull-Rom spline이다. 이름은 Edwin Catmull와 Raphie Rom의 이름에서 유래한다.

 

특징:

• 주어진 점들 위에서 정의됨(interpolation)
• 국소적인 변동 특성(노이즈에 안정적)
• 일차 미분의 연속성

두 점 $P_0$와 $P_1$을 지나는 일반적인 3차의 곡선을 적으면

$$P(t)=a_0+a_{1}t+a_2{t}^2+a_3{t}^3$$

이 곡선이 $t=0$에서 $P_0$을 지나고, $t=1$에서 $P_1$을 지난다고 하더라도, 완전히 결정되지 않는다. 따라서 추가적인 조건을 주어야 하는데, 여기서는 $P_0$와 $P_1$에서의 미분 값이 주어진다고 가정한다. 즉,

$$P(0)=P_0,P(1)=P_1,P^{\prime }(0)=P_0^{\prime },P^{\prime }(1)=P_1^{\prime }$$

이 조건에서 계수들은

$$\begin{gathered} a_0=P_0,a_1=P_0^{\prime }, \\ {a}_2=3(P_1-P_0)-2P_0^{\prime }-P_1^{\prime }, \\ {a}_3=2(P_0-P_1)+P_0^{\prime }+P_1^{\prime } \end{gathered}$$

로 주어진다;

$$P(t)=\left[\begin{array}{cccc}1& t& t^2& t^3\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ -3& 3& -2& -1\\ 2& -2& 1& 1\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_0^{\prime }\\ P_1^{\prime }\end{array}\right]$$

그러나  미분 값을 직접 정해서 넣는 것은 문제가 있다.

 

4 이상의 점들이 주어지는 경우에는 컨트롤상에서의 미분 값을 그 점 주위의 두 점을 있는 직선의 기울기 값으로 근사 시킬 수 있다:

$$P_i^{\prime }⟶(P_{i+1}-P_{i-1})/2$$

이 미분 값을 사용하면 네 개의 컨트롤 점 $\{P_{i-1},P_i,P_{i+1},P_{i+2}\}$이 주어진 경우 $P_i(\leftarrow t=0)$와 $P_{i+1}(\leftarrow t=1)$ 사이를 보간하는 곡선은

$$\begin{array}{rl}P(t)& =\left[\begin{array}{cccc}1& t& t^2& t^3\end{array}\right]\left[\begin{array}{rrrr}1& 0& 0& 0\\ 0& 0& 1& 0\\ -3& 3& -2& -1\\ 2& -2& 1& 1\end{array}\right]\left[\begin{array}{c}{P}_i\\ P_{i+1}\\ (P_{i+1}-P_{i-1})/2\\ (P_{i+2}-P_i)/2\end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{cccc}1& t& t^2& t^3\end{array}\right]\left[\begin{array}{rrrr}0& 2& 0& 0\\ -1& 0& 1& 0\\ 2& -5& 4& -1\\ -1& 3& -3& 1\end{array}\right]\left[\begin{array}{c}{P}_{i-1}\\ P_i\\ P_{i+1}\\ P_{i+2}\end{array}\right]\end{array}$$

로 표현된다. 다시 정리하면

$$P(t)=\frac{1}{2}[2P_i+(-P_{i-1}+P_{i+1})t+(2P_{i-1}-5P_i+4P_{i+1}-P_{i+2})t^2$$

$$+(-P_{i-1}+3P_i-3P_{i+1}+P_{i+2})t^3]$$

로 쓸 수 있는데, 이는 각각의 입력점 사이 구간에서 매개변수를 이용해서 표현하기 좋은 꼴이다. 만약 매개변수를 knots으로 주어지는 경우는 다음과 같은 형식으로 바꾸어서 사용하는 것이 편리하다.

$$P(t)=b_0(t)P_{i-1}+b_1(t)P_i+b_2(t)P_{i+1}+b_3(t)P_{i+2}$$

$$\begin{array}{rl}{b}_0(t)& =\frac{1}{2}(-3t^3+2t^2-t)\\ b_1(t)& =\frac{1}{2}(3t^3-5t^2+2)\\ b_2(t)& =\frac{1}{2}(-3t^3+4t^2+t)\\ b_3(t)& =\frac{1}{2}(t^3-3t^2+3t-1)\end{array}$$

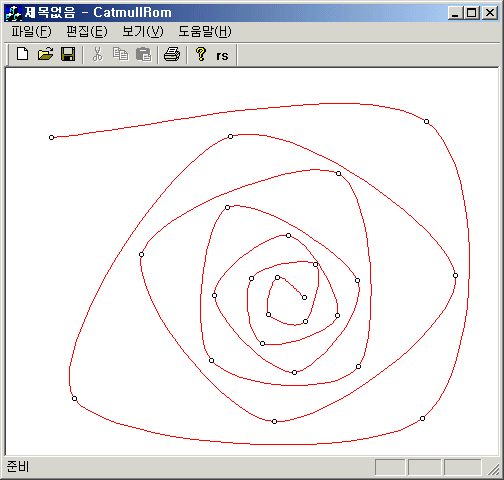
열린 곡선으로 보간을 하는 경우 처음과 끝 구간에는 미분 값을 구할 수 없으므로 정의가 안되지만, 나머지 구간에서는 주어진 점들을 연결하는 충분히 부드러운 곡선이 된다. 양 끝 구간의 보간은 동일점을 반복함으로써 전체적인 구간에서 잘 정의되게 만들 수 있다(끝점에서 기울기를 그 점과 인접점과의 기울기/2로 잡는 것과 같은 효과임). 닫힌 곡선인 경우에는 모든 구간에서 잘 정의가 된다. Catmull-Rom spline은 Bezier나 B-Spline 곡선의 경우와 다르게 컨트롤 점의 convex hull 내부에서만 정의되는 특성을 따르지 않는다.

CPoint CRSpline(double t, CPoint p1, CPoint p2, CPoint p3, CPoint p4) {
    double tt = t * t ;
    double ttt = tt * t ;
    double x = 0.5 * ((-p1.x + 3 * p2.x - 3 * p3.x + p4.x) * ttt
        + (2 * p1.x - 5 * p2.x + 4 * p3.x - p4.x) * tt
        + (-p1.x + p3.x) * t
        + 2 * p2.x);
    double y = 0.5 * ((-p1.y + 3 * p2.y - 3 * p3.y + p4.y) * ttt
        + (2 * p1.y - 5 * p2.y + 4 * p3.y - p4.y) * tt
        + (-p1.y + p3.y) * t
        + 2 * p2.y);
    return CPoint(int(x + .5), int(y + .5)) ;
}

//open spline의 drawing;
void DrawCatmullRom(std::vector<CPoint>& Q, CDC* pDC) {  
#define STEPS (20)
    if (Q.size() < 4) return ;
    CPen red(PS_SOLID, 1, RGB(0xFF, 0, 0));
    CPen *pOld = pDC->SelectObject(&red);
    const int n = Q.size();
    for (int i = 0; i < n - 1; i++) {
        pDC->MoveTo(Q[i]);
        // i = 0 인 경우에는 처음 점을 반복, i = n - 2인 경우에는 마지막 점을 반복..
        int ip = max(i - 1, 0);
        int inn = min(i + 2, n - 1);
        for (int it = 1; it <= STEPS; it++)
            pDC->LineTo(CRSpline(double(it)/STEPS, Q[ip], Q[i], Q[i + 1], Q[inn]));
    };
    pDC->SelectObject(pOld);
}

**네이버 블로그 이전;