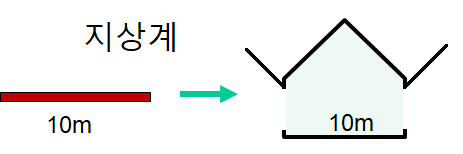
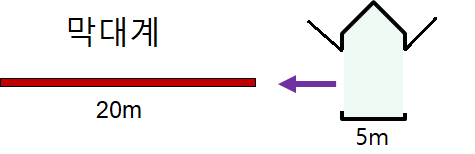
고유길이가 $L_0$인 우주선이 역시 같은 고유길이를 가진 정지한 우주정거장 플랫폼을 일정한 속도로 통과하려 한다. 그런데 우주선의 앞부분에는 폭탄이 설치되어 있어 폭탄이 정거장 플랫폼을 빠져나오는 순간 폭발하도록 되어 있다. 다행히도 우주선의 뒷부분에는 센서가 달려있어 뒷부분이 플랫폼에 들어서는 순간 폭탄의 기폭장치를 끄는 신호를 보낸다.

정거장에서 보면 우주선의 길이가 플랫폼 길이보다 줄어들므로 우주선 뒤쪽이 플랫폼에 들어서는 순간 앞쪽은 여전히 플랫폼 내부에 있으므로 폭탄은 작동하지 않지만 기폭장치를 끄는 센서는 작동하므로 폭발하지 않는다. 한편 우주선에서 보면 플랫폼의 길이가 우주선보다 짧아지므로 우주선의 앞이 플랫폼을 나오는 순간에도 뒤쪽은 여전히 플랫폼에 들어와 있지 않으므로 기폭장치가 꺼지지 않아 결국 폭발한다. 어느 쪽이 맞는가? 틀린 쪽은 어떤 사실을 간과하고 있는가?
'Physics > 상대성' 카테고리의 다른 글
| 시계의 눈금 차이는? (0) | 2025.02.18 |
|---|---|
| Pole-Barn Paradox(코끼리를 냉장고에 넣는 물리적인 방법) (0) | 2025.02.17 |
| 공이 열차를 가로지르는 데 걸리는 시간은? (0) | 2025.02.16 |
| 상대론적 열차의 속도는? (0) | 2025.02.13 |
| 달리는 열차 앞 뒤의 시계를 동시에 사진 찍으면? (1) | 2023.01.06 |