Geometry & Recognition

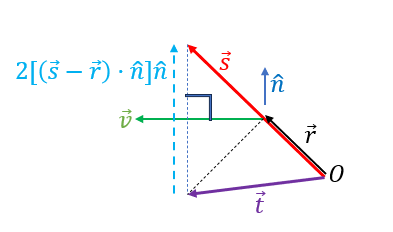
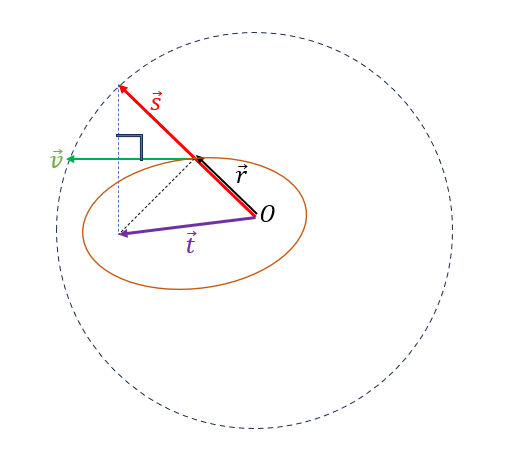
케플러의 1법칙을 행성에 작용하는 힘이 태양에서 거리의 제곱에 반비례하는 중심력(따라서 각운동량이 보존되며, 행성이 위치벡터가 단위시간 동안 휩쓴 면적이 일정하다)이라는 사실만을 이용해서 기하학적 방법으로 유도해 보자.

우선 행성이 태양을 기준으로 미소각 $\Delta \theta$ 만큼 이동했을 때 위치벡터가 쓸고 간 면적은 

\[ \Delta A = \frac{1}{2} r^2\Delta \theta   \]

각운동량 보존에 의해 단위시간당 쓸고 간 면적이 일정하므로 $\Delta t$초 동안 쓸고 간 면적은 

\[ \Delta A = \frac{\ell }{2} \Delta t\]

여기서 $\ell$은 단위질량당 각운동량이다. 따라서 

\[ \Delta t =  \frac{1}{\ell} r^2 \Delta \theta \]

행성이 힘이 받으므로 속도의 변화가 생기는데 뉴턴의 2법칙과 힘이 거리의 제곱에 반비례한다는 사실을 이용하면

\[ \Delta \vec{v} = \frac{\vec{F}}{m} \Delta  t = -\frac{k}{\ell}  \Delta \theta \hat{r}  = \frac{k}{\ell} \Delta \hat \theta\]

여기서 $k =GM_\text{sun}$, $\Delta \hat\theta = -\Delta \theta \hat{r}$임을 이용했다. 이 식을 속도벡터 공간에서 보면 속도의 변화가 크기의 변화는 없고 방향만 일정하게 바뀜을 보여준다. 즉, 속도벡터 공간에서는 속도벡터의 끝은 반지름 $k/\ell$인 원을 그린다. 따라서 속도벡터는 원의 중심 $\vec{c}$에 반지름 벡터 $\frac{k}{\ell}\hat{\theta}$을 더한 식으로 표현된다.

\[ \vec{v} = \vec{c} + \frac{k}{\ell} \hat{\theta}\] 거리의 제곱에 반비례하는 중심력을 받는 행성 궤도 운동의 hodograph가 원이 됨을 보인 것이다. 

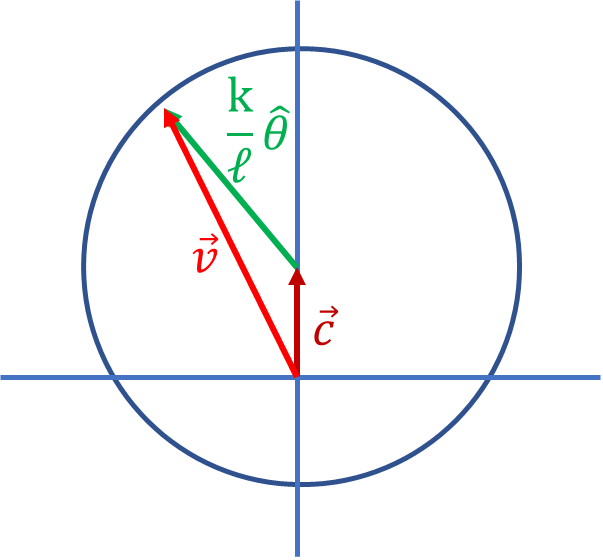
속도벡터 공간에서 속도변화는 원의 접선방향($\hat{\theta}$)이지만 위치벡터 공간에서는 $-\hat{r}$ 방향이므로 행성의 궤도를 구하기 위해서 반시계방향으로 90도 회전된 속도벡터를 이용하자. 각운동량 방향이 $\hat{k}$이므로 회전된 속도벡터는

\[ \vec{u}  = \hat{k} \times \vec{v}\]

그리고 회전된 hodograph의 반지름 벡터는  

\[ \vec{z} \equiv \hat{k} \times \left( \frac{k}{\ell} \hat{\theta} \right) = - \frac{k}{\ell} \hat{r} \]

속도벡터 공간에서 속도의 회전의 중심(속도벡터의 시작)이 반드시 원의 중심이 아닐 수 있으므로 원의 중심에서 회전중심의 차이는 상수가 된다. 이를 구하기 위해서 회전된 벡터에서 회전된 반지름 벡터를 빼면

$$ \vec{d} \equiv \hat{k}\times \vec{c}= \vec{u}- \vec{z}= \vec{u} + \frac{k}{\ell} \hat{r}$$

이는 Laplace-Runge-Lenz 벡터이고 당연히 상수벡터이다.

이제 행성의 궤도가 conic section임을 보이자. $\vec{d} - \vec{u}= \frac{k}{\ell} \hat{r}$의 양변에 $\vec{r}$을 내적하면

$$ LHS = \vec{r} \cdot \vec{d} - \vec{r} \cdot(\vec{k}\times \vec{v}) = \vec{r}\cdot \vec{d} +\ell$$

$$ RHS = \frac{k}{\ell} r$$

좌변식은 위치 $\vec{r}$에서 $\vec{d}$을 법선으로 하는 직선 $\vec{d} \cdot \vec{r}+\ell=0$ 까지의 부호를 포함하는 거리 $D$는 

$$ D = \frac{\vec{d}\cdot\vec{r} + \ell }{|\vec{d}|}$$이므로 

$$ \vec{d} \cdot \vec{r} +\ell= D |\vec{d} |$$로 쓸 수 있다. 그러면 위의 식은

$$ \frac{\text{한 점에서 거리}=r}{\text{한 직선까지거리}=D} = \frac{ k/\ell}{|\vec{d}|} = \frac{k}{\ell d}=\text{const}$$즉 행성의 궤도가 이심률이 $e= k/\ell d$인 conic section의 정의를 만족시키고 있다.

그러면 $d$의 크기는 어떻게 알 수 있는가?

$$ \vec{v}\cdot\vec{v} = \vec{u}\cdot\vec{u} = \left( \vec{d} - \frac{k}{\ell}\hat{r} \right)^2 = d^2 + \frac{k^2}{\ell^2} - 2 \frac{k}{\ell} \vec{d}\cdot \hat{r} = d^2 - \frac{k^2}{\ell^2} + 2\frac{k}{r}$$

$$\to~~\varepsilon  \equiv \frac{1}{2}v^2 - \frac{k}{r} = \frac{1}{2} \left(d^2 - \frac{k^2}{\ell^2} \right)$$로 표현되고 우변이 상수이므로 역학적 에너지가 보존됨을 확인할 수 있다. $d$는 역학적에너지와 각운동량을 이용해서 얻을 수 있다.

$$ d^2 = 2\varepsilon + \frac{k^2 }{ \ell^2 }$$

그리고 $\ell/d=\ell/c$가 초점에서 준선까지 거리를 나타낸다.

Kepler의 제1법칙은 행성의 궤도가 태원이며, 태양이 그 초점 중 하나에 놓인다는 사실을 말한다. 여기서는 뉴턴 역학에서의 보존법칙을 이용하여 기하학적인 증명을 보이도록 한다. 행성에 작용하는 힘이 중심력이므로 (단위질량당) 각운동량이 보존되고, 행성의 운동은 하나의 평면 안에서 일어남을 의미한다.

$$ \vec\ell = \vec r \times \vec v= \text{const}$$

그리고 중력이 보존력이므로 (단위질량당) 역학적에너지 역시 시간에 대해서 일정하게 유지된다.

$$ \varepsilon = \frac{1}{2} v^2 - \frac{k}{r} = \text{const} ~~~~\quad\quad( k=GM_\text{sun})$$

행성이 공간적으로 일정한 영역 안에서 운동하기 위해서는 역학적 에너지가 음수, $\varepsilon <0$이어야 한다. 이는 행성의 속도가 유한하며, 행성이 원점(태양)으로부터 무한히 멀어질 수 없음을 의미한다. 따라서 궤도는 원점을 중심으로 하는 어떤 유한한 영역 내부에 제한된다. 속도가 0일 때 원점에서 가장 멀어질 수 있는데 그 거리가 $R=- k /\varepsilon$이다. 즉, 원점을 중심으로 하고 반지름 $R$인 원 $C$ 내부에 궤도가 제한된다. 행성의 위치벡터 방향으로 $C$의 원주 위의 점을 $\vec{s}$라면

$$ \vec{s} = - \frac{k}{\varepsilon} \frac{\vec{r}}{r}$$

역학적에너지가 보존되므로 이 벡터의 크기는 시간에 무관함은 당연하다.

$$ s=|\vec{s}| = \frac{k }{|\varepsilon|}=\text{const}$$

행성위치에서 접선에 대한 $\vec{s}$의 대칭위치를 $\vec{t}$라고 할 때 이를 구해보자. 우선 $\vec n = \vec{v} \times \vec{\ell}$이라면 이는 행성 위치에서 접선에 수직인 방향이 된다. 따라서 $\vec{t}$는 

$$ \vec{t}  = \vec{s} - 2 \big[ ( \vec{s}- \vec{r} ) \cdot \vec{n} \big] \frac{\vec{n}}{n^2}$$

으로 쓸 수 있다.

우선

$$ (\vec{s}-\vec{r})\cdot \vec{n}=  -( \varepsilon+ k/r) \frac{\ell^2}{\varepsilon}$$

$$ n^2 =  v^2 \ell^2 = 2 (\varepsilon + k/r) \ell^2$$

이므로

$$ \vec{t} = -\frac{k}{\varepsilon} \frac{\vec{r}}{r} + \frac{1}{\varepsilon} \vec{v} \times \vec{\ell} = \frac{1}{\varepsilon} \vec{d}$$

여기서 $\vec{d}$는 Laplace-Runge-Lenz vector로 이 역시 보존이 된다. 따라서 $\vec{t}$는 상수벡터이다.

이제 행성의 위치에서 $\vec{t}$까지 거리($|\vec{r}-\vec{t}|$)와 원점까지 거리($|\vec{r}-0|$) 합이 일정함을 보이자. 즉 행성의 위치는 $\vec{t}$와 원점을 초점으로 하는 타원궤도에 있음을 보일 수 있다. 우선 그림에서 

$$ | \vec{r}-\vec{t}| = |\vec{r}-\vec{s}|$$

$$ | \vec{r}- \vec{s}| + |\vec{r}| = |\vec{s}|$$

이므로

$$ |\vec r - \vec{t}| + |\vec{r} - 0| = \frac{k}{|\varepsilon|}=\text{const}$$이어서 헹성의 위치벡터가 장축의 길이가 $k/|\varepsilon|$인 타원 상에 있음을 명확히 보여준다.

천문학자 Brahe의 정교한 행성관측에 기반해서 Kepler는 태양계에서 행성의 궤도운동에 관한 3가지 법칙을 유추해 냈다. 이후 뉴턴은 만유인력 법칙과 뉴턴의 제 2법칙을 이용해서 만든 미분방정식을 직접적으로 풀어서 확인할 수 Kepler의 법칙을 확인할 수 있었다. 여기서는 미분방정식을 이용하는 접근보다는 행성운동에서 시간이 흘러도 변하지 않고 일정한 값을 가지는 보존량을 찾고 이를 이용해서 행성이 타원궤도를 따라 운동을 함을 보이자.

태양을 원점으로 하여 행성의 위치벡터를 $\vec r$라 두고, 그 크기를 $r = |\vec r|$라 하자. 이때 $\vec r$의 방향을 나타내는 단위벡터를
\begin{equation}
\vec u \equiv \frac{\vec r}{r}
\end{equation}로 정의하면,
\begin{equation}
\vec r = r \vec u
\end{equation}로 쓸 수 있다. 이를 시간에 대해 미분하면 행성의 속도벡터는
\begin{equation}
\vec v = \dot{\vec r}
= \dot r\,\vec u + r\,\dot{\vec u}
\end{equation} 가 된다. 행성은 태양의 중력에 의해 운동하므로, 뉴턴의 제2법칙에 따라 가속도는
\begin{equation}
\vec a = -\frac{k}{r^2}\vec u, \qquad
k \equiv G M_{\text{sun}}
\end{equation}로 주어진다. 가속도가 항상 위치벡터 $\vec r$와 평행하므로, 단위질량당 각운동량 벡터
\begin{equation}
\vec \ell \equiv \vec r \times \vec v
\end{equation}는 보존된다. 실제로 양변을 시간에 대해 미분하면
\begin{equation}
\frac{d\vec\ell}{dt}
= \vec v \times \vec v + \vec r \times \vec a
= \vec r \times \vec a
= 0
\end{equation} 임을 확인할 수 있다. 이제 $\vec\ell$을 보다 구체적으로 계산하면,
\begin{align}
\vec\ell
&= (r\vec u)\times(\dot r\,\vec u + r\,\dot{\vec u}) \\
&= r^2\,\vec u \times \dot{\vec u}
\end{align}
를 얻는다. 한편 $\vec u\cdot\vec u = 1$을 미분하면
\begin{equation}
\vec u\cdot\dot{\vec u} = 0
\end{equation}이므로 $\dot{\vec u}$는 항상 $\vec u$에 수직이다. 이 결과를 이용하여 $\vec a \times \vec\ell$을 계산하면,
\begin{align}
\vec a \times \vec\ell
&= -\frac{k}{r^2}\,\vec u \times (r^2\,\vec u \times \dot{\vec u}) \\
&= k\,\dot{\vec u}
\end{align} 가 된다. 또한 $\vec\ell$이 상수벡터이므로
\begin{equation}
\vec a \times \vec\ell
= \frac{d}{dt}(\vec v \times \vec\ell)
\end{equation}로 쓸 수 있으므로 다음과 같은 벡터 방정식을 얻는다.
\begin{equation}
\frac{d}{dt}\bigl(\vec v \times \vec\ell - k\,\vec u\bigr) = 0,
\end{equation} 따라서 \begin{equation}
\vec{d} \equiv \vec v \times \vec\ell - k\,\vec u 
\end{equation}로 놓으면, $\vec d$는 상수벡터이다. $\vec d$는 Laplace-Runge-Lenz 벡터로 불리우면 힘이 거리의 제곱에 반비례하는 중심력의 형태일 때 각운동량, 역학적 에너지 이외에 추가적으로 보존이 되는 물리량이다. 각운동량 $\vec\ell$은 궤도 평면에 수직이므로, $\vec v \times \vec\ell$은 궤도 평면 내에 놓인다. 따라서 $\vec{d}$도 궤도 평면에 있는 벡터가 된다. 좌표계를 적절히 선택하여 궤도 평면을 $xy$-평면으로, $\vec d$를 $x$축 방향으로 두자.
\begin{equation}
\vec d = (d,0,0)
\end{equation}극좌표계에서
\begin{equation}
\vec r = (x,y,0) = (r\cos\theta, r\sin\theta, 0), \qquad \vec{u}=(\cos \theta , \sin \theta, 0)
\end{equation} 로 두면, $\ell^2$는 
\begin{align}
\ell^2
&= \vec\ell\cdot\vec\ell \\
&= (\vec r\times\vec v)\cdot\vec\ell \\
&= \vec r\cdot(\vec v\times\vec\ell) \\
&= r\,\vec u\cdot(k\,\vec u + \vec d) \\
&= k r + r d \cos\theta
\end{align}를 얻는다. 이를 $r$에 대해 정리하면 행성의 궤도 방정식은
\begin{equation}
r  = \frac{\ell^2/k}{1 + (d/k)\cos\theta}
\end{equation}로 주어지며, 이는 태양을 초점으로 하는 원뿔곡선의 극좌표에서 방정식이다. 기하학적으로 $\ell^2/k$는 초점에서 근일점까지 거리이고 $e\equiv d/k$는 이심률로 $d/k < 1$이면 행성 궤도는 타원이다. 근일점($\theta=0$)의 방향이 $\vec d$의 방향이므로 Laplace-Runge-Lenz 벡터는 행성궤도가 평면에서 놓여있다는 것을 알려줄 뿐만 아니라 궤도의 방향까지도 알려준다.

$\vec{d}$의 제곱을 계산하면 단위질량당 행성의 에너지 $\varepsilon$가 다음을 만족함을 보일 수 있다.

\begin{align} d^2 &= (\vec{v} \times \vec{\ell})^2 - 2 k \vec{u} \cdot (\vec{v} \times \vec{\ell}) + k^2 \\ &=2 \left( \frac{1}{2} v^2 - \frac{k}{r} \right) \ell^2 + k^2 & \\ & = {2\varepsilon} \ell^2  + k^2 \end{align} 따라서 이심률 $e=d/k$가 $0$과 $1$ 사이의 값을 가지면 행성의 에너지가 음의 값을 가져 그 궤도는 타원이 되고, $e=0$이면 포물선 궤도를, 그리고 $e > 1$면 쌍곡선 궤도를 그리게 된다.

$\vec{d}$의 방향이 타원궤도의 근일점을 방향을 의미한다고 했고 궤도방정식을 보면 $d/k$가 이심률을 나타냄을 보았다. $d/k$의 기하학적 의미를 운동방정식과 각운동량 보존을 이용해서 직접적으로 보이도록 하자. 새로운 벡터 $\vec{s}$을 다음과 같이 정의하자.

$$ \vec{s}\equiv \vec{d} \times {\vec{\ell}} = - \ell ^2 \vec{v} + k \vec{\ell}  \times  \vec{u}$$ $\vec{d}$가 상수벡터이므로 $\vec{s}$도 상수벡터이다. 또는 $\vec{s}$를 직접 미분해서 확인할 수 있다.

$$ \dot{\vec{s}} = -\ell^2  \vec{a} + k {\vec{\ell}}    \times \dot{\vec{u}}= -\ell^2  \vec{a} +k     \vec{\ell} \times \frac{ \vec{a}\times \vec{\ell}}{k} = 0 $$

근일점($\vec{r}_1$)과 원일점($\vec{r}_2$)에서 $\vec{s}$를 계산하면

$$ \vec{s} = -\ell ^2 \vec{v}_1 + k {\vec \ell}  \times \vec{u}_1 = - \ell^2 \vec{v}_2 + k {\vec\ell} \times \vec{u}_2$$인데 그 두 지점에서 $\vec{\ell}\times \vec{u}$와 $\vec{v}$는 같은 방향을 가리키고, $\vec{v}_1 \parallel - \vec{v}_2$이므로 두 지점에서 크기가 

$$ -\ell^2 v_1 + k\ell  = -(-\ell^2 v_2 +k \ell)~~\to ~~ \frac{2k}{\ell}= v_1 + v_2 = \frac{\ell}{r_1} + \frac{ \ell}{r_2} = \frac{r_1 +   r_2 }{ r_1  r_2} \ell $$이어서 각운동량은 근일점과 원일점까지의 거리로 표현할 수 있다. $$ \ell^2 = 2k \frac{ r_1 r_2}{r_1+r_2}$$ 이 결과를 근일점이나 원일점에서 계산한 $\vec{d}$에 대입하면 $$ d = k - \frac{\ell^2}{r_2} = k \frac{r_2 - r_1}{r_1 + r_2 } $$이어서 $d/k$가 이심률임이 명확하게 보인다.