물체가 충돌하기 직전 장력은

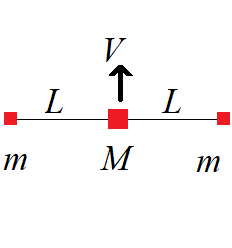
그림과 같이 3 물체가 줄(전체 길이=$2L$)로 연결되어 있다. 물체 $M$에 충격을 주어 줄에 수직한 방향으로 $V$의 속도로 움직이기 시작한다. 질량 $m$인 두 물체가 충돌하기 직전 줄에 걸리는 장력은?

힌트: 외력이 없으므로 운동량이 보존된다. 충돌 직전 두 물체의 수직 속도 성분 $v_{\mathrm{\perp }}$은 같아야 하고, 수평성분의 크기($v_{||}$)도 같아야 한다. 운동량 보존에 의해서 

$$y:MV=(M+2m)v_{\mathrm{\perp }}\to v_{\mathrm{\perp }}=\frac{1}{1+2m/M}V$$

역학적에너지 보존에 의해서

$$\frac{1}{2}M{V}^2=\frac{1}{2}M{v}_{\mathrm{\perp }}^2+m(v_{\mathrm{\perp }}^2+v_{||}^2)\to v_{||}=\sqrt{\frac{1}{1+2m/M}}V$$

충돌 직전 $M$의 가속도를 $a$(아랫방향), 줄의 장력을 $T$라면 

$$a=\frac{2T}{M}$$

이고 $M$과 같이 움직이는 관찰자(비관성계) 입장에서 두 질량 $m$은 충돌직전 순간적으로 원운동을 한다. 이 때 작용하는 구심력은 장력과 관성력(위쪽방향)의 합이다.

$$T+ma=\frac{m{v}_{||}^2}{L}\to T=\frac{m}{(1+2m/M{)}^2}\frac{V^2}{L}$$