Geometry & Recognition

점집합을 일반적인 2차 곡선으로 피팅하는 경우에 방정식은

$$ a x^2 + by^2 + cxy +d x + ey +f = 0$$

의 계수를 주어진 데이터를 이용하여서 구해야 한다. 실제 문제에서는 타원, 포물선 쌍곡 선등의 타입에 따라 몇 가지 제약 조건을 넣어 피팅을 한다. 원은 타원의 특별한 경우로 일반적으로 $a = b$, $c = 0$의 제약 조건이 필요하다. 그러나 보다 엄밀하게 제약을 하게 되면 $a = b = 1$의 추가 조건을 줄 수 있다. 이 경우는 점들이 모두 일직선에 있는 경우를 ($a = b = 0$) 취급할 수 없게 된다. 이 예외적인 경우를 제외하고는 최소자승법을 사용하면 계수를 매우 쉽게 구할 수 있기 때문에 많이 이용된다.

문제: 주어진 데이터를 fitting 하는 이차곡선(원)

$$x^2  + y^2 + A x + B  y + C = 0$$

의 계수 $A, B, C$를 최소자승법을 사용해서 구하라. 

주어진 점집합이 원 위의 점이면 우변이 0이 되어야 하나, 실제 데이터를 얻는 과정에서 여러 노이즈에 노출되므로 일반적으로 0이 되지 않는다. 최소자승법은 주어진 점들이 원에서 벗어나는 정도의 제곱 합이 최소가 되도록 하는 계수 $A, B, C$를 결정한다.  원과 점의 편차의 제곱합
$$ L=\sum_ i   \left |x_i^2 + y_i^2 + A x_i + B y_i + C \right|^2 , $$

의 극값을 찾기 위해서 $A, B,$ 그리고 $C$에 대해 미분을 하면

$$\frac{\partial L}{\partial A} = 2 \sum_i (x_i^2 + y_i^2 + A x_i + B y_i + C) x_i = 0, $$

$$\frac{\partial L}{\partial B} = 2 \sum_i (x_i^2 + y_i^2 + A x_i + B y_i + C) y_i = 0, $$

$$\frac{\partial L}{\partial C} = 2 \sum_i (x_i^2 + y_i^2 + A x_i + B y_i + C) = 0. $$

이 연립방정식을 풀면  $A, B, C$를 구할 수 있다. 계산을 단순하게 만들고 수치적 안정성을 높이기 위해 입력점들의 질량중심 

$$ m_x = \frac{1}{N} \sum_i x_i, \quad m_y = \frac{1}{N} \sum_i y_i$$

계에서 계산을 하자. 이를 위해 입력점의 $x$, $y$ 성분에서 각각 $m_x$, $m_y$만큼을 빼준 값을 좌표값으로 대입하면 된다: 

$$ x_i \to x_i - m_x,\quad y_i \to y_i - m_y$$

그러면 질량중심 좌표계에서는 $S_x = \sum_i x_i =0$, $S_y= \sum_i y_i =0$이 된다.

우선 세 번째 식에서 

$$ C = -\frac{S_{x^2} + S_{y^2}}{N} $$

을 얻을 수 있고, 첫번째와 두 번째 식에서는 각각

$$ S_{x^2} A +  S_{xy} B = -  (S_{x^3} + S_{xy^2})  $$

$$ S_{xy}  A  + S_{y^2} B = - (S_{y^3} + S_{x^2 y} )$$

을 얻을 수 있다. 이를 풀면

$$ A = \frac{- S_{y^2} ( S_{x^3} + S_{xy^2}) + S_{xy} (S_{y^3} + S_{x^2y})  }{ S_{x^2} S_{y^2} - S_{xy}^2 } $$

$$ B= \frac{-S_{x^2}(S_{y^3} + S_{x^2 y}) +S_{xy}  (S_{x^3} + S_{xy^2}) }{S_{x^2} S_{y^2}- S_{xy}^2} $$

여기서 주어진 데이터의 각 차수에 해당하는 moment는 아래처럼 계산된다:

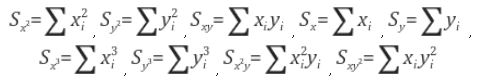
추정된 원의 중심 $(c_x, c_y)$는 

$$ c_x = - \frac{A}{2},   \qquad c_y = - \frac{B}{2} $$

로 주어지고, 반지름은 

$$r^2 =  c_x^2 +c_y^2 - C = c_x^2 + c_y^2 + \frac{1}{N}( S_{x^2}+S_{y^2})$$

로 주어진다.

Ref: I. Kasa, A curve fitting procedure and its error analysis. IEEE Trans. Inst. Meas., 25:8-14, 1976

/* 구현 코드: 2024.04.01, typing error 수정 & 질량중심계 계산으로 수정;*/
double circleFit_LS(std::vector<CPoint> &Q, double &cx, double &cy, double &radius) {
    if (Q.size() < 3) return -1;
    double sx2 = 0.0, sy2 = 0.0, sxy  = 0.0;
    double sx3 = 0.0, sy3 = 0.0, sx2y = 0.0, sxy2 = 0.0;
    double mx = 0, my = 0;            /* center of mass;*/
    for (int k = Q.size(); k-->0;)
        mx += Q[k].x, my += Q[k].y;
    mx /= Q.size(); my /= Q.size();
    /* compute moments; */
    for (int k = Q.size(); k-->0;) { /* offset (mx, my)*/
        double x = Q[k].x - mx, xx = x * x;
        double y = Q[k].y - my, yy = y * y;
        sx2  += xx;      sy2  += yy;      sxy  += x * y;
        sx3  += x * xx;  sy3  += y * yy;
        sx2y += xx * y;  sxy2 += yy * x;
    }
    double det = sx2 * sy2 - sxy * sxy;
    if (fabs(det) < 1.e-10) return -1;    /*collinear한 경우임;*/
    /* center in cm frame; */
    double a = sx3 + sxy2;
    double b = sy3 + sx2y;
    cx = (sy2 * a - sxy * b) / det / 2;
    cy = (sx2 * b - sxy * a) / det / 2;
    /* radius squared */
    double radsq = cx * cx + cy * cy + (sx2 + sy2) / Q.size();
    radius = sqrt(radsq);
    cx += mx; cy += my; /* recover offset; */
    return fitError(Q, cx, cy, radius);
}

https://kipl.tistory.com/357

https://kipl.tistory.com/32

Savitzky-Golay 필터는 일차원의 데이터에 대해 이동평균을 취하는 경우와 같은 방식으로 동작하는 필터이지만, 윈도의 모든 점에 동일한 가중치를 주는 이동평균과 다르게 윈도 픽셀 값을 보간하는 다항식을 최소자승법으로 찾아서 해당 지점의 값으로 할당하는 방식을 택한다(frequency domain에서 분석하면 Savitzky-Golay 필터의 특성, 예를 들면, 피크의 위치가 잘 유지되는 점과 같은 특성을 좀 더 다양하게 볼 수 있다). 이 필터를 쓰기 위해서는 다항식의 찾수와 윈도 크기를 정해야 한다. (다항식의 찾수가 정해지면 최소 윈도 크기는 정해진다).

동일한 방식으로 이차원에 대해서도 Savitzky-Golay를 적용할 수 있다. 이 경우 다항식은 $(x, y)$의 2 변수 함수로 2차원 평면에서 정의되는 곡면으로 나타낸다. 2차원 영상의 경우도 국소 필터를 사용할 수 있지만, 필터 윈도를 영상 전체로 잡아서 전 영역을 보간하는 곡면을 찾을 수도 있다. 배경 조명이 균일하지 않는 영상의 경우 이 곡면을 이용하면 조명에 의한 효과를 예측할 수 있고, 이를 보정한 영상을 이용하면 인식에 도움을 받을 수 있다. (문자 인식에서 문서를 스캔할 때 생기는 균일하지 않은 배경이나, 2차원 바코드 인식에서 배경의 추정 등 다양한 부분에서 사용할 수 있다. 좀 더 간단하게는 배경의 변화를 균일하게 기울어진 평면으로 근사를 하여 추정할 수 있다) 

3차 다항식으로 영상을 보간하는 경우: \begin{align} I(x, y)&= a_{00}\\ &+a_{10} x + a_{01} y \\ &+a_{20} x^2 + a_{11} xy + a_{02} y^2\\ &+a_{30} x^3+a_{21} x^2y+a_{12} xy^2+a_{03} y^3, \quad (x, y)\in \mbox {image} \end{align}

다항식은 $x= [a_{00}, a_{10},..., a_{03}]^T$ 의 10개의 필터 계수를 추정하면 얻어진다. 추가적으로 Savitzky-Golay을 이용하면 영상의 미분 값을 쉽게 구할 수 있다. 로컬 버전의 필터인 경우에 필터 적용 값은 윈도의 중심인 $(x, y) = (0, 0)$에서 다항식 값인 $a_{0}$이다. 이 지점에서 $x$-방향의 편미분 값은 $a_{10}$, $y$-방향의 편미분 값은 $a_{01}$로 주어진다.

필터의 계수 $x$는 최소자승법을 적용하면 얻을 수 있다. 위의 다항식에 $N(= width\times height)$개의 픽셀로 구성된 영상의 각 픽셀에서 좌표와 픽셀 값을 대입하면, $N$개의 식을 얻는다. 이를 행렬로 표현하면, 

$$\bf A\cdot x = b$$

$\bf A$는 $N\times10$ 의 행렬로 각 행은 픽셀의 좌표로 구해진다: 

$${\bf A} =\left[ \begin{array}{cccccccccc} 1&x_0&y_0&x_0^2&x_0y_0&y_0^2&x_0^3&x_0^2y_0&x_0y_0^2&y_0^3\\ 1&x_1&y_1&x_1^2& x_1y_1& y_1^2& x_1^3& x_1^2 y_1 & x_1 y_1^2 & y_1^3\\ 1& x_2& y_2 &x_2^2 & x_2 y_2& y_2^2 & x_2^3 & x_2^2 y_2 & x_2 y_2^2 & y_2^3 \\ &&&&\vdots \end{array} \right]$$

여기서, $i$-번째의 픽셀 위치가 $(x_i, y_i)$로 주어진 경우다. $\bf b$는 $N$-(열) 벡터로 각 픽셀 위치에서 픽셀 값을 나타내는 벡터다: 

$${\bf b}=\left[\begin{array}{c} I(x_0, y_0)\\I(x_1,y_1)\\I(x_2, y_2)\\ \vdots \end{array}\right]$$

최소자승법을 적용하면, 추정된 다항식의 계수 벡터 $\bf x$는 $|\bf A\cdot x - b|^2$을 최소로 하는 벡터로,

$$\bf x = (A^T \cdot A)^{-1} \cdot A^T \cdot b$$

로 주어짐을 알 수 있다. $\bf A^T \cdot A$는 $10\times 10$의 대칭 행렬로 역행렬은 쉽게 구할 수 있다.

이렇게 추정된 2차원 곡면은 영상에서 추정된 배경의 픽셀 값 분포를 의미한다. 문자인식의 예를 들면, 보통 경우에 흰 배경에 검은색 활자를 인식한다. 스캔된 영상에 검은색 활자 때문에 추정된 곡명은 일반적으로 주어진 픽셀이 만드는 곡면보다도 낮게 된다. 픽셀 값이 추정된 곡면보다 더 낮은 픽셀들은 보통 검은색 문자들을 의미하므로, 이 차이의 평균값을 구하면, 대략적으로 어떤 픽셀이 배경에 속하는지 (곡면과 차이가 평균보다 작고, 또한 픽셀 값이  곡면의 아래에 놓인 경우), 아니면 문자 영역인지(곡면과 차이가 평균보다 크고, 픽셀 값이 곡면의 아래에 놓인 경우)를 구별할 있게 된다.   

이제 이 정보들을 이용해서 추정을 다시 하는데 이번에는 1차 추정에서 글씨 영역으로 분류된 픽셀을 제외하고 배경을 추정하면 좀 더 정확한 배경을 기술하는 곡면을 얻을 수 있다.
로컬 필터로 사용할 때는 1차원에서와 마찬가지로 필터 계수를 lookup table로 만들어서 사용할 수 있으나, 전 영역을 대상으로 할 때는 행렬의 크기가 매우 커져서 연산량도 많아진다. 

영상:

1차 추정 배경 영상:

2차 추정 배경 영상:

두 영상 사이의 perspective 변환은 8개의 매개변수 $(a, b, c, d, e, f, g, h)$에 의해서 다음 식처럼 기술이 된다. (see, http://kipl.tistory.com/86)

또는, 

따라서, 매개변수를 찾기 위해서는 두 영상에서 서로 대응하는 점이 4개 이상 주어져야 한다. N개의 대응점들이 주어진 경우

각각의 대응점을 위의 식에 대입해서 정리하면 아래의 행렬식을 얻을 수 있다.(좌변 행렬의 마지막 열은 전부 - 부호가 들어가야 한다) 
 

또는, 간단히 

$$ \bf A \cdot x = b$$

로 쓸 수 있다. 그러나 대응점을 찾을 때 들어오는 noise로 인해서 실제 데이터를 이용하는 경우에는 정확히 등호로 주어지지 않는다. 따라서, 실제 문제에서는 좌변과 우변의 차이의 제곱을 최소로 만드는 $\bf x$를 찾아야 할 것이다.

$$ \mathbf{x}^{*} = \underset{\mathbf{x}}{\text {argmin }} | \mathbf{A}\cdot \mathbf{x} - \mathbf{b}|^2.$$

최소자승해를 찾기 위해 $\bf x^{T}$에 대해 미분을 하면

$$ \bf (A^{T} \cdot A)\cdot x  = A^{T} \cdot b,$$

를 얻고, 이 식을 풀어서 ${\bf x}^*$을 구하면 된다. $\bf A^T \cdot A$는 $8\times 8$의 대칭 행렬로 역행렬을 구할 수 있다 (주어진 점들 중 한 직선 위에 놓이지 않는 점이 4개 이상이 있어야 한다). 따라서 최소자승해는 다음과 같이 쓸 수 있다:

$$\bf x^{*} = (A^{T} \cdot A)^{-1} \cdot (A^{T} \cdot b).$$