update:2024.10.28
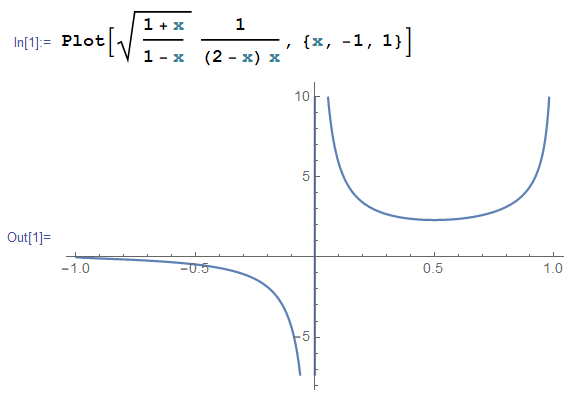
$$ I = \text{Pr}\int_{-1}^1 \sqrt{ \frac{1+x}{1-x}} \frac{1}{(2-x)x} dx$$
복소함수
$$f(z)=\left(\frac{1+z}{1-z} \right)^{1/2}\frac{1}{(2-z)z}$$
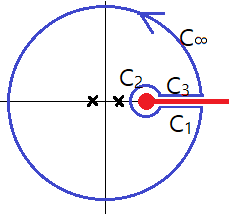
의 contour $\Gamma$에 대한 적분을 고려한다. $z=\pm1$이 branch point이고, $z=0,2$은 simple pole이다. cut line은 그림처럼 잡고, 위상은 $$0 \le \arg(z+1) \le 2\pi,\quad -\pi \le \arg(1-z)\le \pi $$로 선택한다.
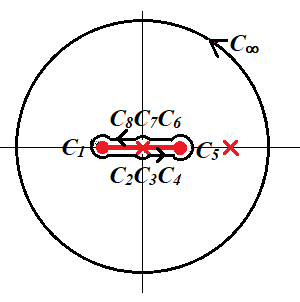
residue 정리에 의해서
$$ \int_\Gamma f(z) dz = \left(\oint_{C_\infty} - \sum \int _{C_i} \right)f(z) dz = 2\pi i \times \text{Res}(z=2) = \sqrt{3} \pi \\ \to ~~ \sum \int_{C_i} f(z) dz =- \sqrt{3}\pi $$
$C_1$: $z+1=\epsilon e^{i \theta}$ $$\int_{C_1} f(z)dz = O(\sqrt{\epsilon}\epsilon)\rightarrow 0$$
$C_5$: $z-1=\epsilon e^{i \theta}$ $$\int_{C_5} f(z)dz = O(\sqrt{\epsilon})\rightarrow 0$$
$C_3$: $$z=\epsilon e^{i \theta}~(\theta: \pi \rightarrow 2\pi)\\z+1= e^{i2\pi}\\z-1= e^{-i\pi}\to 1-z= e^{i0}$$이므로
$$\sqrt{\frac{1+z}{1-z}} =\sqrt{\frac{e^{i2\pi }}{e^{i0}}} = e^{i \pi} \\ \to \quad \int_{C_3} f(z) dz = e^{i \pi} \int_{\pi}^{2\pi} \frac{i \epsilon e^{i\theta}}{2\epsilon e^{i \theta}} d\theta =- i \frac{\pi}{2}.$$
$C_7$: $$z=\epsilon e^{i\theta}~(\theta:0 \rightarrow \pi)\\z+1=e^{i0}\\ z-1= e^{i\pi} \to 1-z = e^{i0}$$이므로
$$\sqrt{\frac{1+z}{1-z}} =\sqrt{\frac{e^{i0}}{e^{i0}}} = 1 \\ \to \quad \int_{C_7} f(z) dz = \int_0^\pi \frac{i\epsilon e^{i \theta}}{2\epsilon e^{i \theta}} d\theta =i \frac{\pi}{2} $$
$C_2 + C_4$: $$z+1= (x+1) e^{2i \pi }~(x: -1 \rightarrow 1) \\z-1=(1-x)e^{-i\pi} \to 1-z=(1-x) e^{i0}$$이므로
$$\int_{C_2 + C_4} = e^{i \pi} \int_{-1}^{1} \sqrt{\frac{1+x}{1-x}}\frac{dx}{(2-x)x}=-I.$$
$C_6 + C_8$: $$z+1= (x+1) e^{i 0}~(x: 1 \rightarrow -1)\\z-1=(1-x)e^{i\pi} \to 1-z=(1-x)e^{i 0}$$이므로
$$\int_{C_6 + C_8} = \int_{1}^{-1} \sqrt{\frac{1+x}{1-x}}\frac{dx}{(2-x)x}= - I$$
$C_\infty$: $z= R e^{i \theta}$ $$ \int_{C_\infty} f(z)dz = O( 1/R) \rightarrow0.$$
이 결과를 모두 정리하면,
$$ I =\text{Pr} \int_{-1}^1 \sqrt{\frac{1+x }{1-x}} \frac{dx}{(2-x)x}=\frac{\sqrt{3}}{2}\pi.$$
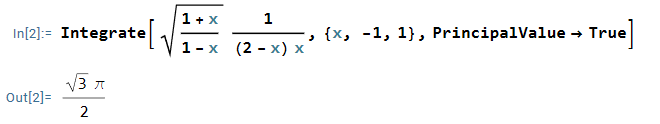
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-014 (0) | 2022.01.03 |
|---|---|
| Integration along a branch cut-013 (0) | 2021.12.22 |
| Integration along a branch cut-011 (0) | 2021.01.04 |
| Integration along a branch cut-010 (0) | 2021.01.04 |
| Integration along a branch cut-009 (0) | 2021.01.03 |