Integration along a branch cut-010

update: 2024.10.28;

$$ I = \int_{-1}^1 \sqrt{1-x^2} dx$$

복소함수를 $f(z)= \sqrt{z^2-1}$으로 선택하면, $z=\pm i$가 branch point이므로 cut line을 $z=-i$와 $z=+i$을 잇는 선분으로 잡는다. 위상은 $$-\frac{\pi}{2} \le \arg(z-i),~\arg(z+i)  \le \frac{3\pi}{2} $$로 선택하면 된다. $z=\infty$에서 residue가 있으므로 그림과 같은 contour에서 적분을 고려하자. 

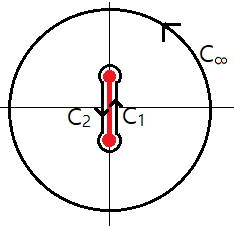
$C_\epsilon(z=i)$, $C_{\epsilon'}(z=-i)$: $$ \int f(z) dz = O(\sqrt{\epsilon} \epsilon) \rightarrow  0.$$

$C_1$: $$z- i = (1-x)e^{-i \pi/2}  \\z+i = (1+x)e^{i\pi/2}~(x:-1\to 1)$$이므로

$$\int_{C_1}   = \int_{-1}^{1}\sqrt{1-x^2}  d( e^{i \pi/2} x) = i I$$

$C_2$: $$z-i = (1-x)e^{i 3\pi/2} \\ z+i=(1+x)e^{i\pi/2}~(x:1\to-1)$$이므로

$$\int_{C_2}  = \int_{1}^{-1} \sqrt{1-x^2} e^{i\pi}   d (e^{i\pi/2}x) = i I$$

무한대에서 residue를 결정하기 위해서

$$ \sqrt{z^2-1} = z \sqrt{1-1/z^2 } = z - \frac{1}{2z}+ \cdots \\ \int_{C_\infty} f(z) dz =  2\pi i \times \frac{1}{2} =  i \pi $$

residue 정리에 의해서 $$\int _{C_\infty} f(z)dz = \sum \int_{C_i} f(z) dz$$이므로

$$ I = \int_{-1}^1 \sqrt{1-x^2} dx  =\frac{\pi}{2}.$$

이 결과는 $x=\sin \theta$의 치환적분을 이용하면 더 쉽게 구할 수 있다.