Integration along a branch cut-009

$$I = \int_{-\infty}^\infty \frac{p e^{ipr} dp}{\sqrt{p^2 + m^2 }  } \quad   (r>0,~m>0)$$

복소함수 $$f(z) =\frac{z e^{izr} }{\sqrt{z^2 + m^2}}$$의 contour 적분을 이용한다. $z=\pm im$가 $f(z)$의 branch point이므로 그림과 같이 cut line을 잡는다(적분은 upper half plane에서 한다). 위상은 $$-\frac{3\pi}{2} \le \arg(z-im)\le \frac{\pi}{2},\quad -\frac{\pi}{2}\le \arg(z+im) \le \frac{3\pi}{2}$$로 선택한다.

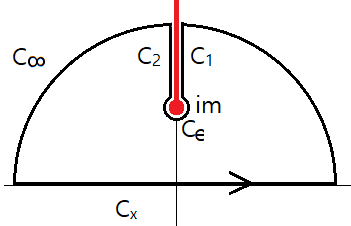
그림의 contour에서 $f(z)$가 analytic하므로 $$\int_\Gamma f(z) dz = 0$$이고, $C_1$: $z-im = (s-m) e^{i \pi/2} ~~(s: \infty\rightarrow m)$, $z+im = (s+m) e^{i\pi/2}$, $z=is$이므로 $$\int_{C_1} f(z) dz = \int_{\infty}^m \frac{  (is) e^{-sr} (ids)}{ \sqrt{s^2 - m^2 } e^{i\pi/2}} = -i \int_m^\infty \frac{s e^{-sr} ds }{ \sqrt{ s^2 - m^2}} .$$

$C_2$: $z-im= (s-m) e^{-i 3\pi/2} ~~(s: m\rightarrow \infty)$, $z+im = (s+m) e^{i \pi/2}$, $z=is$이므로

$$\int_{C_2} f(z) dz = \int_m^\infty \frac{ (is) e^{-sr} (ids) }{ \sqrt{s^2 - m^2 }} e^{-i \pi /2} = -i \int_m^\infty \frac{s e^{-sr}ds }{\sqrt{s^2 - m^2} }.$$

그리고 $$ \int_{C_\epsilon} f(z) dz  = O( \sqrt{\epsilon})\rightarrow 0.$$

$C_\infty$에서 $z=R e^{i\theta} ~(\theta:0\rightarrow \pi)$로 놓으면 $|e^{izr}|  \le  e^{- R \sin \theta r} \rightarrow 0$이므로 

$$\int_{C_\infty} f(z) dz \rightarrow 0.$$

따라서 $x$-축을 따라 적분한 값 $I$는

$$I = \int_{-\infty}^{\infty} \frac{p e^{i p r}dp}{ \sqrt{p^2 + m^2 }} = 2i \int_m^\infty \frac{se^{-sr} ds} {\sqrt{s^2 - m^2}} =i\times \text{positive number}.$$ 우변의 적분은 closed form으로 표현할 수는 없지만 0이 아님은 알 수 있다. 그리고 real 함수에 대한 적분이므로 수치적으로 다룰 때 훨씬 계산하기 쉬운 형태가 되었다.