Otsu 알고리즘은 이미지를 이진화시키는데 기준이 되는 값을 통계적인 방법을 이용해서 결정한다. 같은 클래스(전경/배경)에 속한 픽셀의 그레이 값은 유사한 값을 가져야 하므로 클래스 내에서 픽셀 값의 분산은 되도록이면 작게 나오도록 threshold 값이 결정되어야 한다. 또 잘 분리가 되었다는 것은 클래스 간의 거리가 되도록이면 멀리 떨어져 있다는 의미이므로 클래스 사이의 분산 값은 커야 함을 의미한다. 이 두 가지 요구조건은 동일한 결과를 줌을 수학적으로 보일 수 있다.
이미지의 이진화는 전경과 배경을 분리하는 작업이므로 클래스의 개수가 2개, 즉, threshold 값이 1개만 필요하다. 그러나 일반적으로 주어진 이미지의 픽셀 값을 임의의 개수의 클래스로 분리할 수도 있다. 아래의 코드는 주어진 이미지의 histogram을 Otsu의 아이디어를 이용해서 nclass개의 클래스로 분리하는 알고리즘을 재귀적으로 구현한 것이다. 영상에서 얻은 히스토그램을 사용하여 도수를 계산할 수 있는 0차 cumulative histogram($\tt ch$)과 평균을 계산할 수 있는 1차 culmuative histogram($\tt cxh$)을 입력으로 사용한다.
$$ {\tt thresholds}= \text {argmax} \left( \sigma^2_B = \sum_{j=0}^{nclass-1} \omega_j m_j^2 \right)$$
* Otsu 알고리즘을 이용한 이미지 이진화 코드: kipl.tistory.com/17
* 좋은 결과를 얻으려면 히스토그램에 적당한 필터를 적용해서 smooth하게 만드는 과정이 필요하다.
// 0 <= start < n;
double histo_partition(int nclass, double cxh[], int ch[], int n, int start, int th[]) {
if (nclass < 1) return 0;
if (nclass == 1) {
int ws; double ms;
if (start == 0) {
ws = ch[n - 1];
ms = cxh[n - 1] / ws;
} else {
ws = ch[n - 1] - ch[start - 1]; // start부터 끝까지 돗수;
ms = (cxh[n - 1] - cxh[start - 1]) / ws; // start부터 끝까지 평균값;
}
th[0] = n - 1;
return ws * ms * ms; // weighted mean;
}
double gain_max = -1;
int *tt = new int [nclass - 1];
for (int j = start; j < n; j++) {
int wj; double mj;
if (start == 0) {
wj = ch[j];
mj = cxh[j]; //mj = cxh[j] / wj;
}
else {
wj = ch[j] - ch[start - 1]; //start부터 j까지 돗수;
mj = (cxh[j] - cxh[start - 1]); //mj = (cxh[j] - cxh[start - 1]) / wj;
}
if (wj == 0) continue;
mj /= wj; //start부터 j까지 평균;
double gain = wj * mj * mj + histo_partition(nclass - 1, cxh, ch, n, j + 1, tt);
if (gain > gain_max) {
th[0] = j;
for (int k = nclass - 1; k > 0; k--) th[k] = tt[k - 1];
gain_max = gain;
}
}
delete [] tt;
return gain_max;
};trimodal 분포의 분리;
class0: 0~th[0]
class1: (th[0]+1)~th[1],
class2: (th[1]+1)~th[2]=255
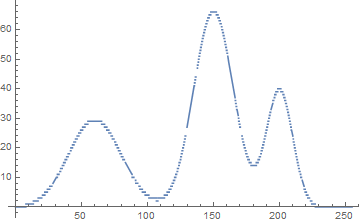

// recursive histo-partition 테스트;
// 0--t[0];--t[1];...;--t[nclass-2];t[nclass-1]=255=n-1;
// nclass일 때 threshold 값은 0---(nclss-2)까지;
double GetThreshValues(int hist[], int n, int nclass, int th[]) {
if (nclass < 1) nclass = 1;
// preparing for 0-th and 1-th cumulative histograms;
int *ch = new int [n]; // cdf;
double *cxh = new double [n]; //1-th cdf;
ch[0] = hist[0];
cxh[0] = 0; // = 0 * hist[0]
for (int i = 1; i < n; i++) {
ch[i] = ch[i - 1] + hist[i] ;
cxh[i] = cxh[i - 1] + i * hist[i];
}
// nclass=1인 경우도 histo_partition()내에서 처리할 수 있게 만들었다.
double var_b = histo_partition(nclass, cxh, ch, n, 0, th);
delete [] ch;
delete [] cxh;
return var_b;
}'Image Recognition' 카테고리의 다른 글
| Median-Cut 컬러 양자화 (0) | 2021.01.12 |
|---|---|
| Union-Find 알고리즘을 이용한 영역분할 (0) | 2021.01.11 |
| Kuwahara Filter (2) | 2020.12.28 |
| Moving Average을 이용한 Thresholding (0) | 2020.11.26 |
| Expectation Maximization Algorithm for Two-Component Gaussian Mixture (0) | 2017.01.02 |








