기하 알고리즘을 특히 폴리곤 관련 알고리즘을 테스트하기 위해서는 폴리곤 데이터를 만들어야 한다. 여기서 2차원의 점들을 이용하여 간단히 simple polygon을 만드는 방법을 소개한다.
Simple polygon을 만들기 위해서는 점들을 정렬을 해야 한다. 각 점들을 $x$ 축으로 정사영하면 $x$축 방향에 대해 정렬이 된다(같은 $x$ 값인 경우에는 $y$의 크기대로 정렬). 따라서 x 값으로 정렬된 점들을 순차적으로 연결하면 하나의 polyline을 만들 수 있다. polyline의 끝을 잇는다고 해서 simple polygon이 항상 만들어지지는 않는다. 이를 해결하기 위해서는 점들을 한 직선을 기준으로 위-아래로 분리하고, 직선의 윗부분은 $x$ 값이 큰 순서대로 정렬을 하고, 아래 부분은 $x$ 값이 작은 순서대로 정열을 하면 폴리 라인이 아닌 simple polygon을 얻을 수 있다. 직선은 어떻게 잡을까? 이것은 가장 작은 $x$ 값을 갖는 점과 가장 큰 $x$ 값을 같은 점을 잇는 직선을 생각하면 편리하다.
// cross(CB, AB)
// A->B-C: 반시계(C가 AB 왼편: > 0), 시계(C가 AB오른편: < 0), 일직선(0);
int CCW(const CPoint& A, const CPoint& B, const CPoint& C) {
const CPoint CB = C - B, AB = A - B;
return CB.x * AB.y - CB.y * AB.x;
}
// x가 커지는(같으면 y가 커지는) 순서로 정렬;
bool compare(const CPoint &a, const CPoint& b) {
if (a.x == b.x) return a.y < b.y;
return a.x < b.x;
}
std::vector<CPoint> makeSimplePolygon(const std::vector<CPoint>& pts) {
if (pts.size() < 1) return std::vector<CPoint> (); //null_vector;
int rightId = 0, leftId = 0;
for (int i = pts.size(); i-->1;) {
if (pts[i].x > pts[rightId].x) rightId = i;
if (pts[i].x < pts[leftId].x) leftId = i;
}
std::vector<CPoint> LP, RP;
for (int i = 0; i < pts.size(); i++) {
if (i == rightId || i == leftId) continue;
// 기준선의 왼편(LP)/오른편(RP)에 놓인 점 분리;
if (CCW(pts[leftId], pts[rightId], pts[i]) >= 0) LP.push_back(pts[i]);
else RP.push_back(pts[i]);
}
if (LP.size() > 0) std::sort(LP.begin(), LP.end(), compare);
if (RP.size() > 0) std::sort(RP.begin(), RP.end(), compare);
std::vector<CPoint> sploy;
spoly.reserve(LP.size()+RP.size()+2);
spoly.push_back(pts[leftId]);
for (int i = 0; i < LP.size(); i++) spoly.push_back(LP[i]);
spoly.push_back(pts[rightId]);
for (int i = RP.size(); i-->0;) spoly.push_back(RP[i]);
// spoly = clockwise simple polygon;
return spoly;
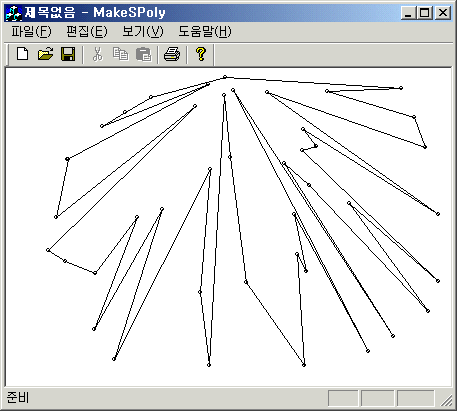
};다른 방법으로는 위와 같은 직선을 만들고, 아랫부분의 점들의 convex hull을 구성하고, 나머지 점들을 마찬가지의 방법으로 정렬을 하여 폴리곤을 만들거나, 아니면 한 점을 잡아서(맨 아래 오른쪽) 그 점을 기준으로 해서 나머지 점들을 각도에 대해서 정렬을 한 다음 그 정렬된 순서대로 폴리곤을 구성하면 된다.
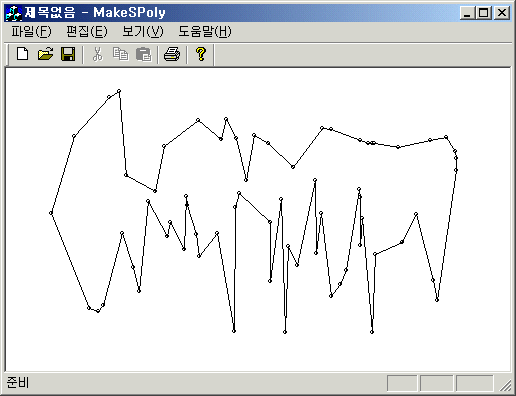
기준점에 대한 각도를 정렬하여서 만든 예(동일한 각도가 생기는 경우에는 기준점에서의 거리로 비교)
**네이버 블로그에서 이전;
'Computational Geometry' 카테고리의 다른 글
| Minimum Bounding Rectangle (3) | 2021.03.15 |
|---|---|
| Minimum Enclosing Circle (0) | 2021.03.01 |
| 단순 다각형의 Convex Hull (0) | 2021.01.24 |
| 단순 다각형의 무게중심 (0) | 2021.01.24 |
| 단순 다각형의 면적(2D) (0) | 2021.01.23 |




