$$I = \int_{-1}^{1} \frac{\log (a+x)dx}{x \sqrt{1-x^2}} = 2\pi \arctan\left( a - \sqrt{a^2-1} \right) \qquad a>1$$
$x= \cos \theta $로 치환을 하면
$$ I = \int_0^\pi \frac{\log(a + \cos \theta) d \theta }{\cos \theta} = \frac{1}{2} \int_0^{2\pi} \frac{ \log( a+ \cos \theta) }{\cos \theta }$$를 얻고, $z= e^{i \theta}$로 다시 치환을 하면
$$ I = \frac{1}{i} \oint _\text{unit circle} \frac{ \log(z^2 + 2a z + 1) - \log(2z)}{1+z^2}$$
따라서 $I$를 구하는 문제는 $$ f(z)= \frac{ \log(z^2 + 2a z + 1) - \log(2z)}{1+z^2}$$의 단위원 위에서 경로적분으로 환원이 된다. $\log$함수 때문에 $z= -a \pm \sqrt{a^1-1}, ~0$이 branch point에 해당하므로 그림의 cutline을 선택한다.
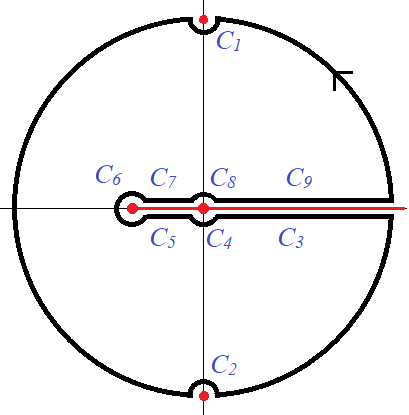
그리고 $z= \pm i$는 $f(z)$의 simple poles에 해당하고, residue는 각각
$$\text{Res}f(\pm i) = \frac{\log (a) + i \pi/2}{\pm 2i}~\to ~ \text{Res}f(i) + \text{Res} f(-i) = 0$$임을 확인할 수 있다. 따라서 $$ \int_{C_1 +C_2} = \pi i \times \left(\text{Res}f(i) + \text{Res}f(-i)\right) =0$$또 $z=0$, $z= -a+\sqrt{a^2-1}$을 감싸는 미소원에서 적분은 0에 수렴함도 확인 할 수 있다. $$ \int_{C_6+C_4 + C_8} = 0$$. $C_3$과 $C_9$에서는 분모의 두 $\log$함수의 위상이 상쇄되므로 0에 수렴함도 알 수 있다. 마지막으로 $C_5$와 $C_7$는 $\log(2z)$의 cutline에 해당하지 않으므로 적분기여가 없으므로,
$$ \int_{C_5 +C_7} = -2\pi i \int_0^{ a-\sqrt{a^2-1}} \frac{dz}{z^2 + 1} = - 2\pi i \arctan \left( a - \sqrt{ a^2-1}\right) $$
따라서
$$ \int_{-1}^1 \frac{ \log(a+x) dx}{x \sqrt{1-x^2} } = 2\pi \arctan\left( a - \sqrt{ a^2-1}\right) $$
'Mathematics' 카테고리의 다른 글
| Integrate 1/(1+sin^2 θ) from 0 to 2π (1) | 2024.12.29 |
|---|---|
| Integration along a branch cut-046 (0) | 2024.12.27 |
| Integration along a branch cut-045 (45) | 2024.12.23 |
| Integration along a branch cut-044 (0) | 2024.12.21 |
| Integration along a branch cut-043 (0) | 2024.12.16 |




