\begin{gather} \int_{-\pi}^\pi \frac{ \theta \sin \theta d \theta }{a+ \sin \theta} = \frac{\pi a}{\sqrt{a^2-1}} \left( \pi - \tan ^{-1} \sqrt{a^2-1}\right) \\ \int_{-\pi}^\pi \frac{ \theta \cos \theta d \theta }{a+ \sin \theta} = 2\pi \log \left( 2a^2 -2a \sqrt{ a^2 -1} \right)\end{gather}
함수 $$f(z) =\frac{2z \log z}{z^2 + 2i a z -1},\qquad a>1$$의 경로적분을 고려하자. Brach point가 $z=0$이므로 음의 $x$ 축을 cutline으로 선택한다. 그러면 $-\pi \le \arg(z) \le \pi $. 적분경로는 그림과 같이 반지름 1인 원으로 선택하자.
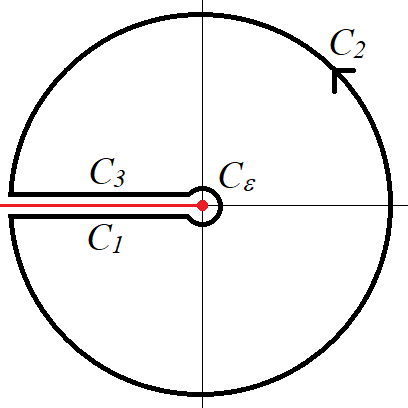
그러면 simple pole $z_1= -i (a- \sqrt{a^2-1})$은 경로 내부에 포함이 된다. 그리고 residue는
$$ \text{Res} f(z_1) = -\frac{(a - \sqrt{ a^2-1}) \big[ \log (a- \sqrt{a^2-1} ) -i \pi/2 \big] }{\sqrt{a^2-1}}$$
경로 $C_1$에서 $ z= x e^{-i \pi}~(x:0\to1)$이므로
$$\int_{C_1} = 2 \int_0^1 \frac{x(\log x - i \pi) dx }{ x^2 - 2iax -1}$$
경로 $C_3$에서 $z= x e^{i\pi}~(x: 1 \to 0)$이므로,
$$ \int_{C_3} = -2 \int_0^1 \frac{x(\log x + i \pi) dx }{x^2 - 2i ax -1}$$이어서
\begin{gather} \int_{C_1+C_3} = - 4\pi i \int_0^1 \frac{xdx}{x^2 - 2ia x-1} \\ =-4\pi i \int_0^1 \frac{(x^2 -1 + 2ia x)xdx}{(x^2-1) ^2 + 4 a^2 x^2 } \\ = -2\pi i \int_{-1}^0 \frac{u du}{u^2 + 4a^2 u + 4a^2} +8 \pi a \int_{0}^1 \frac{ x^2 dx}{(x^2-1)^2 + 4a^2 x^2 }\\ = -2\pi i \left( \log (2a) + \frac{a\log( a - \sqrt{a^2-1}) }{\sqrt{a^2-1}}\right)\\ +\frac{2\pi}{\sqrt{a^2-1}} \left(\frac{\pi}{2} \sqrt{a^2-1} - a\tan^{-1} \sqrt{a^2-1} \right)\end{gather}
그리고 $C_2$에서는 $z= e^{i \theta}~(\theta:-\pi \to \pi)$이므로
\begin{gather}\int_{C_2} = 2\int_{-\pi}^\pi \frac{( i \theta e^{i \theta} ) ( i \theta e^{i \theta} d \theta)}{ e^{2i \theta} + 2i a e^{i \theta} -1} \\= 2\int_{-\pi}^\pi \frac{ i^2 \theta e^{i \theta} d \theta }{e^{i \theta} + 2i a - e^{- i \theta} }\\ = \int_{-\pi}^\pi \frac{ ( - \theta \sin \theta + i \theta \cos \theta) d \theta }{a + \sin \theta}\end{gather}
그리고 $C_\epsilon$에서 적분은 0에 수렴한다. 정리하면
\begin{gather} \int_{-\pi}^\pi \frac{ \theta \sin \theta d \theta }{a+ \sin \theta} = \frac{\pi a}{\sqrt{a^2-1}} \left( \pi - \tan ^{-1} \sqrt{a^2-1}\right) \\ \int_{-\pi}^\pi \frac{ \theta \cos \theta d \theta }{a+ \sin \theta} = 2\pi \log \left( 2a^2 -2a \sqrt{ a^2 -1} \right)\end{gather}
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-047 (0) | 2024.12.29 |
|---|---|
| Integrate 1/(1+sin^2 θ) from 0 to 2π (1) | 2024.12.29 |
| Integration along a branch cut-045 (47) | 2024.12.23 |
| Integration along a branch cut-044 (0) | 2024.12.21 |
| Integration along a branch cut-043 (0) | 2024.12.16 |



