$$I = \int_0^\infty \left( \frac{\arctan x }{ x}\right)^2 dx =\pi \log 2$$

복소함수
$$ f(z)= \left( \frac{\arctan z}{z} \right)^2 = \left(\frac{ \frac{i}{2} \log \frac{1-iz}{1+iz}}{ z }\right) ^2 $$의 경로적분을 고려하자.
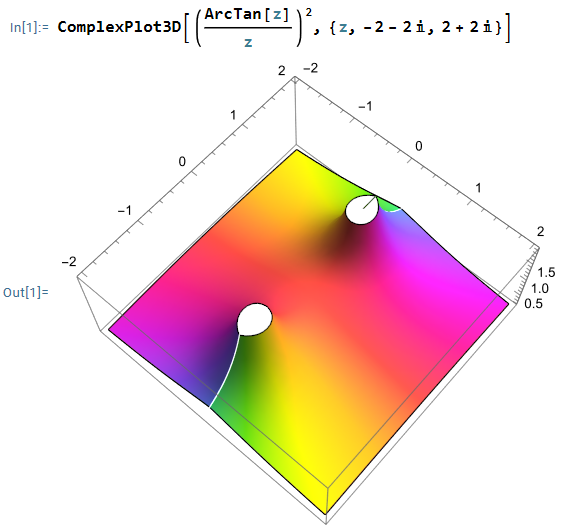
$z= \pm i$가 $\arctan(z)$의 branch point 이므로 그림과 같이 cutline을 선택한다: $-\frac{3\pi}{2}\le \arg(z-i) \le \frac{\pi}{2}$
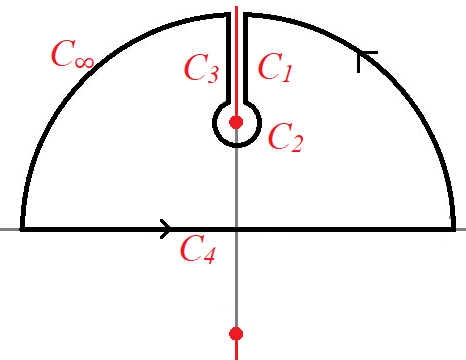
$C_1$과 $C_3$에서 적분은 cutline을 시계방향으로 건널 때 $\log(1+iz)$는 $2\pi$의 위상이 더해짐을 고려하고($\log(1-iz)$는 upper cutline 전후에서 위상변화가 없으므로 $C_1,C_3$에서 적분기여가 없다), $$ \arg(1+iz) = - {\pi}, ~~\arg(1-iz) =0 ~~\text{on}~~C_3$$이므로 \begin{gather}\int_{C_1 + C_3} f(z) dz = - \int_{C_3}\frac{ -\frac{1}{4} (\log|1+iz| +i\pi )^2 +\frac{1}{2} (\log |1+ iz| + i \pi) \log|1-iz|}{z^2}dz \\ + \int_{C_3} \frac{ -\frac{1}{4} ( \log|1+ i z| - i \pi )^2 +\frac{1}{2}(\log | 1+iz| -i \pi) \log|1-i z|}{z^2 }dz \\ = i \pi \int_{C_3} \frac{\log | 1+iz| - \log |1-iz| }{ z^2 }dz \qquad (z= iy) \\ = \pi \int_1^\infty \frac{\log|1-y| - \log|1+y|}{y^2 }dy\qquad (y = 1/u) \\ = \pi \int_0^1 \big( {\log (1-u) - \log(1+u)} \big) du = -2\pi\log 2 \end{gather} $C_\infty, ~C_2$에서 적분은 0에 수렴함을 쉽게 알 수 있다. 따라서 $\oint f(z) dz = 0$에서
$$ I = \frac{1}{2} \int_{C_4} f(z) dz = - \frac{1}{2} \int_{C_1 + C_3} f(z)dz = \pi \log 2$$
'Mathematics' 카테고리의 다른 글
| Integrate 1/(1+sin^2 θ) from 0 to 2π (1) | 2024.12.29 |
|---|---|
| Integration along a branch cut-046 (0) | 2024.12.27 |
| Integration along a branch cut-044 (0) | 2024.12.21 |
| Integration along a branch cut-043 (0) | 2024.12.16 |
| Integrate [ Log(1-x)/x, {x, 0, 1} ] (0) | 2024.12.04 |



