$$ I = \int_0^1 \frac{ \log(1-x) dx}{x}$$ $$f(z) = \frac{\log(1-z)}{z}$$을 그림과 같은 경로를 따라 적분하자.
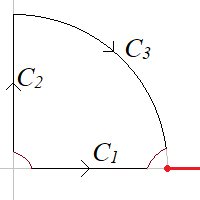
$z=1$이 branch point이므로 cut line을 그림처럼 선택하자. 그림의 폐경로 내에서 $f(z)$가 analytic하고 $I$가 실수값을 가지므로 $$ \left(\int_{C_1} - \sum' \int_{C_k} \right)f(z) dz = 0~~\to ~~ I =\text{Re}\int_{C_2+ C_3 + C_{\epsilon_0} + C_{\epsilon_1}} f(z) dz$$ 경로 $C_2$에서 $z = i y ~(y: 0 \to 1)$이므로
\begin{gather} \text{Re} \int_{C_2} = \text{Re} \int_0^1 \frac{\log(1-i y) (idy)}{iy } =\text{Re}\int_0^1 \frac{\log(1- i y)dy}{y}\\ = \int_0^1 \frac{\log \sqrt{1+ y^2} dy}{y} = \frac{1}{4}\int_0^1 \frac{\log(1+u)du }{u} ~~(\leftarrow u=y^2)\\= \frac{1}{4}\int_0^1 \left( \frac{\log(1-u^2) }{u } - \frac{\log(1-u)}{u}\right) du \\ = \frac{1}{8} \int_0^1 \frac{\log(1-t) dt}{t} - \frac{1}{4}I = -\frac{1}{8} I \end{gather}
경로 $C_3$에서 $z= e^{i \theta} ~( \theta: \frac{\pi}{2}\to 0) $
\begin{gather} \text{Re} \int_{C_3} = \text{Re} \int_{\pi/2}^ 0 \frac{\log (1- e^{i \theta} ) (i e^{i\theta}d \theta )}{ e^{i \theta}}= \text{Im} \int_0^{\pi/2} \log( 1-e^{ i \theta}) d \theta \\= \int_0^{\pi/2} \left( \frac{\theta}{2} - \frac{\pi}{2} \right)d \theta = - \frac{3\pi^2 }{16}\end{gather}
경로 $C_{\epsilon_0 }$에서 $z= \epsilon e^{i \theta}$
\begin{gather}\text{Re} \int_0^{\pi/2} \frac{\log ( 1+ \epsilon e^{i \theta} )(i e^{i \theta} d \theta)}{e^{i \theta}} = -\int_0^{\pi/2} \tan^{-1} \left( \frac{\epsilon \sin \theta }{1-\epsilon \cos \theta} \right) d \theta \to 0\end{gather}
이므로 기여가 없고 마찬가지로 경로 $C_{\epsilon_1}$에서 기여가 없다. 따라서
$$ I = -\frac{1}{8}I -\frac{3\pi^2}{16}~~\to~~ \int_0^1 \frac{\log(1-x) dx }{x} = -\frac{\pi^2}{6}$$
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-044 (0) | 2024.12.21 |
|---|---|
| Integration along a branch cut-043 (0) | 2024.12.16 |
| Integration along a branch cut-042 (1) | 2024.12.02 |
| Shokhotski-Plemelj theorem (0) | 2024.11.26 |
| Integration along a branch cut-041 (0) | 2024.11.25 |



