길이 $L$이 막대가 같은 길이의 줄에 그림과 같이 매달려 있다가 운동을 시작한다. 막대와 바닥사이에 마찰은 없다. 막대의 질량중심 속력의 최댓값은?
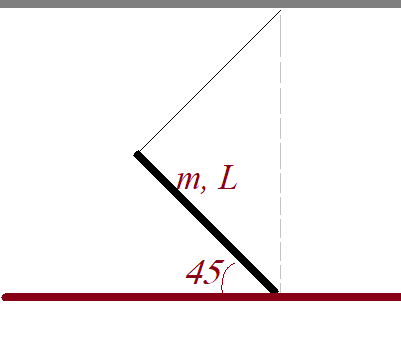
풀이: 막대 맨 아래쪽은 매끄러지고 줄에 연결된 부분은 회전을 하게 된다. 따라서 막대는 질량중심의 병진운동과 더불어 질량중심에 대한 회전운동 에너지를 가지는데, 역학적 에너지 보존에 의해서 처음 위치에너지와 같아야 한다. 병진운동에너지가 최대가 되는 위치는 회전각속도가 0이 되어야 한다. 막대가 가장 아래로 내려온 위치에서 줄은 수직이 되므로 회전각속도가 0이 되어야 한다(회전을 한다면 줄에 연결된 부분이 더 내려가야 하는데 가장 낮은 위치이므로 불가). 이때 바닥 부분과 줄에 연결된 부분의 속도는 같아지고 이 속도가 질량중심 속도와 같다. 역학적 에너지 보존을 이용하면
$$ \Delta U = mg \left ( \frac{\sqrt{2}-1}{2}L - \frac {\sqrt {2}}{4} L \right) = \frac {\sqrt {2}-2}{4} mgL $$
$$\Delta K +\Delta U =0~~~\to ~~ \frac{1}{2}m v_{cm} ^2 + \frac{1}{2}I \cdot 0^2 = \frac {2- \sqrt {2} }{4} mgL$$
$$\to~~~ v_{cm} = \sqrt{\frac{2-\sqrt{2}}{2} gL}$$
이 순간 질량중심의 가속도는? 막대에 대해서 알 수 있는 사실은 막대 top과 bottom의 운동이다. Bottom은 수평운동을 하므로 수평 가속도 성분만 있고, top은 수직과 수평성분을 가질 수 있다. 이 두 지점의 평균이 질량중심의 가속도이고, 이때 막대에 작용하는 힘은 수직성분만 있으므로 top과 bottom의 가속도 수평성분은 서로 반대여야 한다. 따라서 $a_{cm} = \frac{1}{2} a_{top, y}$이고, top 수직가속도는 줄에 매달린 원운동의 구심가속도에 해당한다.
$$ a_{top, y} = \frac{v_{top}^2}{L} = \frac{v_{cm}^2 }{L}~~\to ~~a_{cm} =\frac{1}{2}a_{top, y} = \frac{2-\sqrt{2}}{4} g$$
이 결과와 운동방정식, 그리고 $y_{cm} = \frac{L}{2} \sin\theta$ 관계를 이용하면 이 순간 줄에 걸리는 장력과 바닥의 수직항력을 계산할 수 있다.
'Physics > 역학' 카테고리의 다른 글
| 볼링공이 점프없이 경사면을 내려갈 최대속력은? (0) | 2025.02.27 |
|---|---|
| 막대가 움직이기 시작하는 순간 두 줄의 장력은? (0) | 2025.02.26 |
| 마찰면에서 회전하는 원판의 각가속도는? (0) | 2025.02.24 |
| 달이 부서지지 않고 지구를 돌 수 있는 거리한계는: Roche Limit (0) | 2025.02.24 |
| 고무밴드와 기둥 사이의 마찰계수는? (0) | 2025.02.23 |




