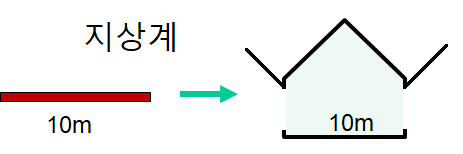
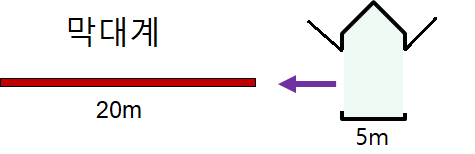
길이가 $L_0 =20$미터 막대를 들고 일정한 속도 $v=\sqrt{3}c/2~(\to~\gamma = 2)$로 앞에 있는 헛간을 향해서 달린다. 헛간의 폭은 $\ell_0=10$미터이고 막대의 앞이 헛간의 뒷문에 도달하는 순간 헛간의 양문이 닫히도록 설계되어 있다. 지상에서 볼 때 막대는 길이수축 때문에 $20/\gamma= 10m$ 길이로 보이므로 막대가 헛간에 완전히 들어갈 수 있고 그 순간 양쪽 문이 닫히면 가둘 수 있다. 그런데 막대를 미는 사람(막대와 같이 움직이는 관찰자)의 입장에서 보면 헛간이 막대를 향해서 $v$의 속력으로 달려오므로 헛간의 폭이 정지해 있을 때의 절반인 $5m$로 줄어들어 보인다. 그러면 막대가 헛간에 갇히는 것은 불가능하지 않는가?

힌트: 지상계에서는 헛간의 문이 동시에 닫히지만, 막대계에서 보면 헛간은 먼 쪽 뒤쪽 문이 막대 앞이 도달한 순간 닫히고, 헛간의 앞문은 나중에 닫힌다(rear clock ahead effect). 그 시간 차이는
$$\frac{\gamma v\ell_0}{c^2} = \frac{2\times \frac{\sqrt{3}c}{2} \times (10m)}{c^2} = \frac{10\sqrt{3}}{c}$$ 그런데 이 시간은 헛간의 앞이 막대의 뒤에 도달한데 걸리는 시간과 같다. 헛간 앞과 막대 뒤의 거리가 $L_0- \frac{\ell_0}{\gamma} = 15m$이고, 헛간이 $v$로 다가오므로 걸리는 시간은 $\frac{15(m)}{v} = \frac {10\sqrt {3}}{c}$ 임을 확인할 수 있다.
반박: 그러면 막대 앞이 헛간의 뒷문에 막히므로 막대가 더 이상 움직이지 못하는 것이 아닌가?(막대계에서는 헛간이 더 이상 다가오지 못하는 것). 뉴턴역학에서는 막대가 반발력을 받으면 막대는 강체이므로 막대의 뒤쪽에서 즉각 힘을 감지할 것이지만(뉴턴역학에서 완전 강체에서 음속은 무한대이다), 특수상대성 이론에서는 모든 정보는 광속보다 빨리 진행될 수 없다. 막대 앞이 헛간 뒷문에서 닿아서 휘어지거나 부서지는 정보가 광속으로 퍼진다면 막대 뒤편에서 알아차리는 데 걸리는 시간은 $\frac {L_0}{c}= \frac {20}{c}$인 데, 이 시간은 헛간 앞쪽이 막대 뒤쪽에 도달하는 데 걸리는 시간 $\frac {10\sqrt {3}}{c}$ 보다 더 길다. 즉, 헛간의 앞이 막대의 뒤에 도달하여서 앞쪽 문이 닫히는 순간까지도 막대의 뒤쪽에서는 앞쪽이 휘어지거나 부서지고 있다는 정보를 알 수 없음을 의미하므로 막대의 뒤쪽은 헛간 앞쪽 문이 닫히기 직전 안으로 일정한 속도로 들어갈 수 있다.
'Physics > 상대성' 카테고리의 다른 글
| 우주선은 폭발을 하는가? (0) | 2025.02.18 |
|---|---|
| 시계의 눈금 차이는? (0) | 2025.02.18 |
| 공이 열차를 가로지르는 데 걸리는 시간은? (0) | 2025.02.16 |
| 상대론적 열차의 속도는? (0) | 2025.02.13 |
| 달리는 열차 앞 뒤의 시계를 동시에 사진 찍으면? (1) | 2023.01.06 |




