평면 위에 점집합이 주어지고 이들을 잘 기술하는 직선의 방정식을 구해야 할 경우가 많이 발생한다. 이미지의 에지 정보를 이용해 선분을 찾는 경우에 hough transform과 같은 알고리즘을 이용하는 할 수도 있지만 수치해석적으로 직접 fitting을 할 수도 있다. 점집합의 데이터를 취합하는 과정은 항상 노이즈에 노출이 되므로 직선 위의 점뿐만 아니라 직선에서 (많이) 벗어난 outlier들이 많이 들어온다. 따라서 line-fitting은 이러한 outlier에 대해서 매우 robust 해야 한다. 데이터 fitting의 경우에 초기에 대략적인 fitting에서 초기 파라미터를 세팅하고, 이것을 이용하여서 점차로 정밀하게 세팅을 해나가는 반복적인 방법을 많이 이용한다. 입력 데이터가 $\{(x_i, y_i)| i=0,..., N-1\}$로 주어지는 경우에 많이 이용하는 최소자승법에서는 각 $x_i$에서 직선상의 $y$ 값과 주어진 $y_i$의 차이(residual)의 제곱을 최소로 하는 직선의 기울기와 $y$ 절편을 찾는다. 그러나 데이터가 $y$축에 평행하게 분포하는 경우를 다루지 못하게 되며, 데이터 점에서 직선까지 거리를 비교하는 것이 아니라 $y$값의 차이만 비교하므로 outlier의 영향을 매우 심하게 받는다.
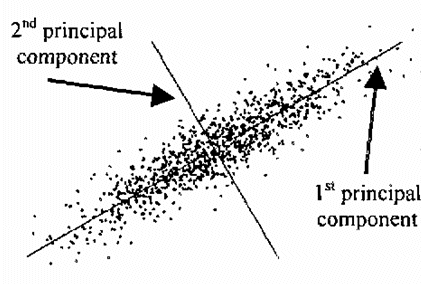
이러한 문제를 제거 또는 완화하기 위해서는 PCA(principal axis analysis)를 이용할 수 있다. 점들이 선분을 구성하는 경우, 선분 방향으로는 점 위치의 편차가 크지만 수직 방향으로는 편차가 상대적으로 작다. 따라서 평면에서 점 분포에 대한 공분산 행렬 $\tt Cov$의 고윳값과 고유 벡터를 구하면, 큰 고윳값을 갖는 고유 벡터 방향이 선분의 방향이 될 것이다.
$$ {\tt Cov}[\{ (x_i, y_i)\}]=\frac{1}{N} \begin{pmatrix} \sum (x_i- \bar{x})^2 & \sum(x_i-\bar{x})( y_i-\bar{y}) \\ \sum (x_i-\bar{x})( y_i-\bar{y}) & \sum (y_i- \bar{y})^2 \end{pmatrix}$$
잘 피팅이 이루어지려면 두 고윳값의 차이가 커야 한다. 또한 outlier에 robust 한 피팅이 되기 위해서는 각 점에 가중치를 부여해서 공분산 행렬에 기여하는 가중치를 다르게 하는 알고리즘을 구성해야 한다. 처음 방향을 설정할 때는 모든 점에 동일한 가중치를 부여하여 선분의 방향을 구한 후 다음번 계산에서는 직선에서 먼 점이 공분산 행렬에 기여하는 weight를 줄여 주는 식으로 하면 된다. weight는 점과 직선과의 거리에 의존하나 그 형태는 항상 정해진 것이 아니다.
// 점에서 직선까지 거리;
double DistanceToLine(CPoint P, double line[4]) {
// 중심에서 P까지 변위;
double dx = P.x - line[2], dy = P.y - line[3];
// 직선의 법선으로 정사영 길이 = 직선까지 거리;
return fabs(-line[1] * dx + line[0] * dy);
}
// PCA-방법에 의한 line-fitting;
double LineFit_PCA(std::vector<CPoint>& P, std::vector<double>& weight, double line[4]) {
// initial setting: weight[i] = 1.;
// compute weighted moments;
double sx = 0, sy = 0, sxx = 0, syy = 0, sxy = 0, sw = 0;
for (int i = P.size(); i-->0;) {
int x = P[i].x, y = P[i].y;
double w = weight[i];
sx += w * x; sy += w * y;
sxx += w * x * x; syy += w * y * y;
sxy += w * x * y;
sw += w;
}
// variances;
double vxx = (sxx - sx * sx / sw) / sw;
double vxy = (sxy - sx * sy / sw) / sw;
double vyy = (syy - sy * sy / sw) / sw;
// principal axis의 기울기;
double theta = atan2(2 * vxy, vxx - vyy) / 2;
line[0] = cos(theta);
line[1] = sin(theta);
// center of mass (xc, yc);
line[2] = sx / sw;
line[3] = sy / sw;
// line-eq:: sin(theta) * (x - xc) = cos(theta) * (y - yc);
// calculate weights w.r.t the new line;
std::vector<double> dist(P.size());
double scale = 0;
for (int i = P.size(); i-->0;) {
double d = dist[i] = DistanceToLine(P[i], line);
if (d > scale) scale = d;
}
if (scale == 0) scale = 1;
for (int i = dist.size(); i-->0; ) {
double d = dist[i] / scale;
weight[i] = 1 / (1 + d * d / 2);
}
return fitError(P, line);
};
void test_main(std::vector<CPoint>& pts, double line_params[4]) {
// initial weights = all equal weights;
std::vector<double> weight(pts.size(), 1);
while (1) {
double err = LineFit_PCA(pts, weight, line_params) ;
//(1) check goodness of line-fitting; if good enough, break loop;
//(2) re-calculate weight, normalization not required.
}
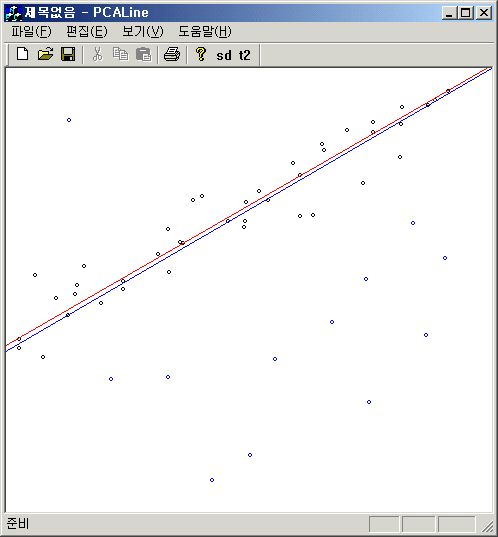
};아래 그림은 weight를 구하는 함수로 $weight= 1 /\sqrt{1+dist\times dist}$를 이용하고, fitting 과정을 반복하여 얻은 결과다. 상당히 많은 outlier가 있음에도 영향을 덜 받는다. 파란 점이 outlier이고, 빨간 직선은 outlier가 없는 경우 fitting 결과고, 파란 선은 outlier까지 포함한 fitting 결과다.
##: 네이버 블로그에서 이전;
'Image Recognition > Fundamental' 카테고리의 다른 글
| Fast Float Sqrt (0) | 2020.12.27 |
|---|---|
| 2차원 Gaussian 분포 생성 (0) | 2020.12.10 |
| Histogram Equalization (0) | 2020.11.12 |
| Least Squares Fitting of Circles (0) | 2020.11.11 |
| Integer Sqrt (0) | 2020.11.11 |








