주어진 점집합을 포함하는 최소 면적의 rectangle을 찾는 문제는 점집합의 convex hull을 포함하는 rectangle을 찾는 문제와 같다. convex hull의 한 변을 공유하면서 전체를 포함하는 rectangle 중 최소 면적인 것을 찾으면 된다. Rotating Caliper를 쓰면 $O(n)$ step이 요구된다.

// 방향이 dir이고 A점을 통과하는 직선과 방향이 dir에 수직이고 B점을 통과하는 직선의 교점을 반환;
CPoint LineIntersect(CPoint A, CPoint dir, CPoint B);
//
#define DOT(A,B) ((A).x*(B).x + (A).y*(B).y))
void BoundingRect(std::vector<CPoint>& hull, CPoint vtx[4]) {//non-optimal.
if (hull.size() < 3) return;
double minArea = DBL_MAX;
int bIndex = 0, tIndex = 0, lIndex = 0, rIndex = 0;
for (int j = 0, i = hull.size() - 1; j < hull.size(); i = j++) {
CPoint &A = hull[i], &B = hull[j];
CPoint BA = B - A; // convex hull의 한 기준변;
CPoint BAnormal = CPoint(-BA.y, BA.x); //(B-A)에 반시계방향으로 수직인 벡터;
double BAsq = DOT(BA, BA);
//기준변과 대척점(antipodal point)을 찾는다: BAnormal방향으로 가장 멀리 떨어진 점
int id = FindAntipodal(BAnormal, hull) ;
CPoint QA = hull[id] - hull[i];
//기준변과 대척점을 통과하는 직선과의 사이거리;
double D1 = fabs(double(DOT(BAnormal, QA))) / sqrt(BAsq);
//left_side_end_point;//기준변 반대방향으로 가장 멀리 떨어진 꼭지점;
int id1 = FindAntipodal(-BA, hull);
//right_side_end_point;//기준변 방향으로 가장 멀리 떨어진 꼭지점;
int id2 = FindAntipodal(BA, hull);
///가장 왼쪽과 가장 오른쪽 꼭지점을 연결하는 선분
CPoint H = hull[id1] - hull[id2];
//기준변 방향으로 정사영하면 두 평행선 사이거리를 줌;
double D2 = fabs(double(DOT(BA,H))) / sqrt(BAsq);
double area = D1 * D2;
if (area < minArea) {
minArea = area;
bIndex = i ; tIndex = id;
lIndex = id1; rIndex = id2;
}
}
//directional vector for base_edge;
CPoint dir = hull[(bIndex + 1) % hull.size()] - hull[bIndex] ;
vtx[0] = LineIntersect(hull[bIndex], dir, hull[lIndex]);
vtx[1] = LineIntersect(hull[tIndex], dir, hull[lIndex]);
vtx[2] = LineIntersect(hull[tIndex], dir, hull[rIndex]);
vtx[3] = LineIntersect(hull[bIndex], dir, hull[rIndex]);
}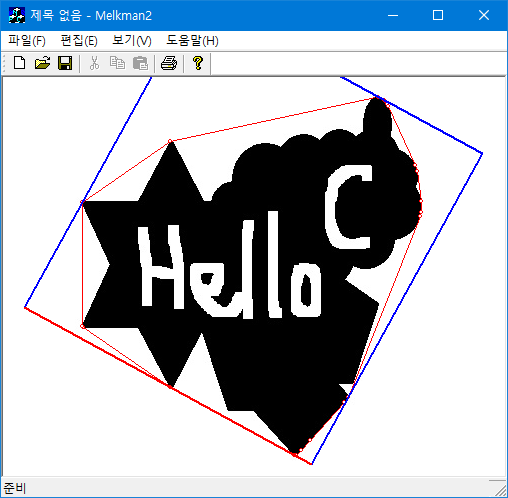
Minimum Volume Box
주어진 점들을 감싸는 최소 면적의 직사각형은 먼저 convex hull을 구한 후 rotating caliper을 써서 구할 수 있다. 다음 코드는 반시계방향으로 정렬된 convex hull을 이용해서 minimum volume box을 구한다.
kipl.tistory.com
728x90
'Computational Geometry' 카테고리의 다른 글
| Jarvis March (0) | 2021.03.26 |
|---|---|
| Approximate Minimum Enclosing Circle (1) | 2021.03.18 |
| Minimum Enclosing Circle (0) | 2021.03.01 |
| Creating Simple Polygons (0) | 2021.01.25 |
| 단순 다각형의 Convex Hull (0) | 2021.01.24 |




