주어진 이미지(destination image)의 일부분($\Omega$)을 다른 이미지(source image: $g(x, y)$)로 자연스럽게 대체하는 seamless blending의 한 기법인 Possion Image Editing을 살펴보자. 수학적으로는 destination image의 한 영역 $\Omega$에서 source image를 보간(interpolation)하는 함수 $f(x,y)$를 찾는 작업이다. $f$는 보간 영역의 경계($\partial\Omega$)에서는 destination image와 같은 컬러 값($f^{*}$)을 가져야 한다.
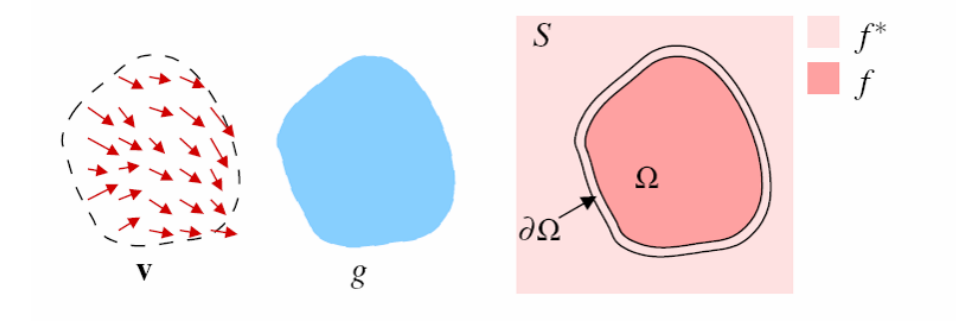
그럼 보간의 기준은 무엇이 되어야 하는가? blending이 잘되기 위해서는 보간 영역에서는 source image와 같은 형상으로 보여야 한다. 이미지에서 형상의 인식은 컬러값 자체가 아니라 컬러의 변화인 gradient에 의해서 결정이 된다. 따라서 보간 함수는 source image의 gradient를 최대한 유지하도록 선택되어야 한다. 이제 seamless blending을 주는 보간 함수를 찾는 문제는 source image가 blending 영역의 경계에서는 destination 이미지의 color값을 가지면서 영역 내부에서는 source image의 gradient 값을 최대한 유지하는 함수를 찾는 변분 문제로 귀결된다: source image의 gradient를 $\mathbf{v}(x, y)=\nabla g= (\partial g/\partial x, \partial g / \partial y)$라 하면,
$$ \underset{f}{\text{argmin}} \iint_{\Omega} | \nabla f - \mathbf{v}|^2 dxdy, \quad\text {with} \quad f = f^*~\text {on}~\partial \Omega.$$
위 식을 $f$에 대해서 variation을 취하면$$\iint 2(\nabla \delta f)\cdot(\nabla f - \mathbf{v}) dxdy = - 2 \iint \delta f ( \nabla^2 f - \nabla \cdot \mathbf{v}) dxdy + 2 \iint \nabla \cdot \left[ \delta f (\nabla f - \mathbf{v})\right] dxdy $$을 얻을 수 있는데 마지막 항은 total derivative이므로 기여가 없다. 따라서 보간함수 $f$는 다음 방정식을 만족해야 한다:
$$ \nabla^2 f = \nabla \cdot \mathbf{v}, \quad \text {or} \quad \frac {\partial^2 f}{\partial x^2} + \frac {\partial ^2 f}{\partial y^2 } = \frac {\partial v_x }{\partial x}+ \frac {\partial v_y}{\partial y}.$$
보간함수를 찾는 과정은 domain $\Omega$에서 Dirichlet boundary condition $f=f^* ~\text {on} ~\partial\Omega$이 부여된 Poisson 방정식의 해를 찾는 것과 같다는 것을 알려준다.
$\nabla \cdot\mathbf{v}= \nabla^2 g$이므로 Poisson 방정식의 해를 $f(x,y)= g(x,y) + h(x,y)$로 쓰면 풀어야 할 문제는 다음의 Laplace 방정식으로 해를 구하는 문제로 바뀐다.
$$ \nabla^2 h = 0, \quad ~~ h|_{\partial\Omega} = (f^* - g)|_{\partial\Omega}$$
** 1차원 예: $f^*(x)=1-\frac{x}{\pi}$, $g(x)=\frac{1}{2} \cos (4x)$ 인 경우, $f(x)=g(x) + h(x)$로 쓰면, $h(x)$는 $h(x=0) = f^*(0) - g(0) = 0.5$, $h(\pi)=f^*(\pi)-g(\pi) = -\frac{1}{2}$의 경계조건을 만족하는 $d^2h/dx^2 = 0$의 해로 주어지는데, $h(x)=\frac{1}{2}- \frac{x}{\pi}$임을 쉽게 알 수 있다. 따라서 $f(x)= \frac{1}{2}-\frac{x}{\pi} +\frac{1}{2} \cos(4x)$로 쓰인다:


'Image Recognition > Fundamental' 카테고리의 다른 글
| Image Moments (0) | 2021.12.04 |
|---|---|
| Orientation 추정 (0) | 2021.11.30 |
| Sampling Theorem (0) | 2021.05.12 |
| Lanczos Resampling (0) | 2021.05.08 |
| Interpolation Kernels (0) | 2021.05.05 |




