$$g(x, y; \sigma)= \frac{1}{2\pi \sigma^2}\exp\left( - \frac{x^2 +y^2 }{2\sigma^2 }\right)$$
원점을 중심으로 분산이 1 인 정규분포를 갖는 평면상의 점을 발생시킬 필요가 있는 경우에 아래의 함수를 이용한다: Box-Muller method.
내장 함수 rand()를 이용하면 $[0,1]$ 구간에서 균일한 분포를 만들 수 있다. $[0,1]\times[0,1]$ 영역에서 균일한 분포를 갖는 두 개의 1차원 랜덤 변수 $x_1$, $x_2$을 이용해서 확률 변수 $y_1$, $y_2$의 2차원 Gaussian 분포를 주는 변환을 구하려면, 우선 확률 보존에 의해서
$$ dx_1 dx_2 = \frac{1}{\sqrt{2\pi}} e^{-y_1^2 /2 } dy_1 \frac{1}{\sqrt{2\pi}} e^{-y_2^2 /2 } dy_2 $$
을 만족시켜야 한다. 극좌표 $\rho^2 = y_1^2 + y_2^2$, $\phi = \tan^{-1}(y_2/y_1)$을 도입하면
$$ dx_1 dx_2 = e^{-\rho^2/2} \rho d\rho \frac{d\phi}{2\pi}$$로 쓸 수 있으므로 미소 변환은
$$ dx_1 = e^{-\rho^2/2} \frac{d\rho^2}{2},\quad dx_2 = \frac{d\phi}{2\pi}$$ 로 선택할 수 있다. 따라서
$$ x_1 = \exp[-\rho^2/2] = \exp[- (y_1^2 + y_2^2 )/2],$$
$$ x_2 = \frac{1}{2\pi} \tan^{-1} (y_2/y_1).$$
그리고, 역변환은
$$ y_1 = \sqrt{-2 \ln (x_1) } \cos (2\pi x_2),\quad y_2 = \sqrt{-2 \ln(x_1) } \sin (2\pi x_2).$$
삼각함수의 계산을 피하기 위해서 반지름이 1인 원 내부에서 정의되는 두 개의 균일한 랜덤 변수 $v_1, v_2$를 도입하면, 다음 변환에 의해서 반지름 1인 원 영역이 변의 길이가 1인 정사각형 영역으로 보내진다.
$$x_1 = R^2(=S) = v_1^2 + v_2^2, \quad 2\pi x_2 = \tan^{-1} (v_2/v_1).$$
따라서 반지름이 1인 원 내부의 랜덤 변수를 써서 2차원의 Gaussian 분포를 만들어주는 변환은
$$ y_1 = \sqrt{-2\ln S} \frac{v_1}{\sqrt{S}}, \quad y_2 = \sqrt{-2\ln S} \frac{v_2}{\sqrt{S}}$$

// 참고; Numerical Receipe;
#define drand() ((double)rand() / RAND_MAX) // [0,1]
// mean = 0; sigma = 1;
void normal_2D(double *x, double *y) {
while (1) {
double V1 = -1. + (2. * drand());
double V2 = -1. + (2. * drand());
double S = V1 * V1 + V2 * V2;
if (S < 1.) {
double rad = sqrt(-2.*log(S) / S);
*x = V1 * rad;
*y = V2 * rad;
/* if (mean, sigma) were given,
*x = meanx + sigma * (*x);
*y = meany + sigma * (*y);
*/
return;
}
}
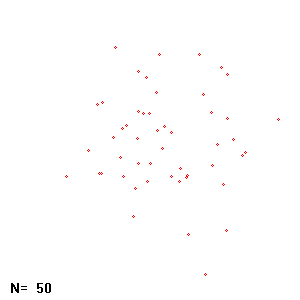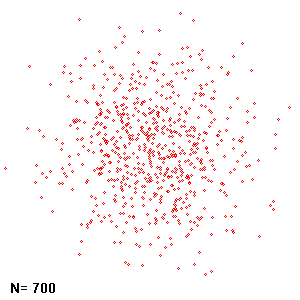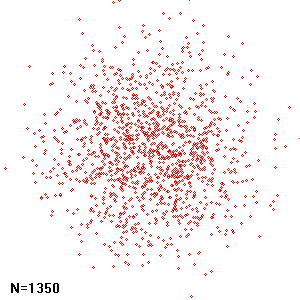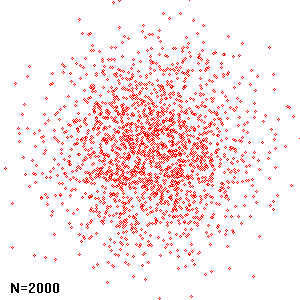
};
'Image Recognition > Fundamental' 카테고리의 다른 글
| 점증적인 cosine/sine 값 계산 (0) | 2020.12.28 |
|---|---|
| Fast Float Sqrt (0) | 2020.12.27 |
| PCA Line Fitting (0) | 2020.11.12 |
| Histogram Equalization (0) | 2020.11.12 |
| Least Squares Fitting of Circles (0) | 2020.11.11 |




