Geometry & Recognition

각 전경 픽셀에 대해서 모든 배경 픽셀까지 거리를 구한 다음 최솟값을 할당하면 된다. 픽셀 수가 n = w * h 개면 time complexity는 O(n^2)이다 (이미지 폭이나 높이의 4승이므로 연산량이 상당하다.) linear time Euclidean distance transform은 kipl.tistory.com/268.

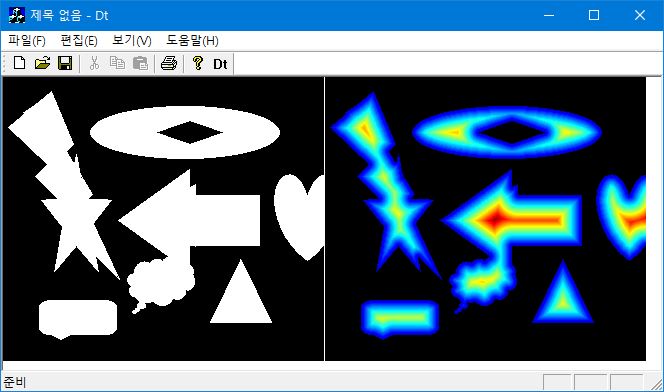
ListPlot3D[ Reverse@ImageData[pic], PlotRange -> Full]

int brute_force_edt(double *img, int w, int h) {
    int *list = new int [w * h];
    int fg_cnt = 0;
    int bg_ptr = w * h;               //배경 픽셀 위치는 끝에서 역으로 채움;
    //전경과 배경 픽셀 위치를 분리;
    for (int i = w * h; i-->0;)
        if (img[i]) list[fg_cnt++] = i;  // foreground;
        else        list[--bg_ptr] = i;  // background;

    for (int i = 0; i < fg_cnt; ++i) {     // 전경 픽셀;
        int xi = list[i] % w, yi = list[i] / w;
        int d2min = INT_MAX;
        for (int j = w * h; j--> fg_cnt;) { // 배경 픽셀까지 거리를 계산해서 최소값을 할당;
                                            // 배경이 list에 역순으로 저장되으로 역방향 서치;
            int dx = (list[j] % w) - xi, dy = (list[j] / w) - yi;
            int dst = dx * dx + dy * dy;
            if (dst == 1) {
            	d2min = 1; break;
            }
            if (d2min > dst) d2min = dst;
        }
        img[list[i]] = d2min;
    }
    delete [] list;
    return fg_cnt;
}

Convex hull은 집합으로 주어진 점이나 영역을 포함하는 가장 작은 볼록 집합이다. 알려진 알고리즘으로는 

1. Jarvis March (Gift Wrap)

2. Graham scan

3. Quick hull (Chain hull)

4. Monotone chain

5.......

여기서는 소개하는 convex hull 알고리즘은 가장 기초적인 알고리즘이다. 두 점에 의해서 만들어지는 선분이 convex hull의 일부이면 나머지 점들은 항상 왼편(설정에 따라 오른편으로 해도 된다)에 있게 된다는 사실을 이용한다. N개의 점이 있을 떄 가능한 선분의 수는 N(N-1) (방향까지 고려함)이고, 나머지 점에 대해서 테스트를 해야 하므로 총 비교 횟수는 N(N-1)(N-2) ~ O(N^3) 정도이다. 알고리즘의 구현이 간단하고, 단순 비교연산이므로 매우 robust해서 점집합의 크기가 작을 때 효과적이다.

static int ccw(CPoint A, CPoint B, CPoint P) ; // cross(AB, AP) > 0 if <ABP> is ccw;

static int ccw(CPoint A, CPoint B, CPoint P) { //cross(AB, AP) > 0 if <ABP> is ccw;
    return ((B.x - A.x) * (P.y - A.y) - (B.y - A.y) * (P.x - A.x));
}

std::vector<CPoint> BruteForceConvexHull(const std::vector<CPoint>& pts) {
    // O(n^3) ;
    if (pts.size() < 3) return std::vector<CPoint> (); //null_vector;
    std::vector<std::pair<int,int>> edges;
    for (int i = 0; i < pts.size(); i++) {
        for (int j = 0; j < pts.size(); j++) {
            if (pts[j] == pts[i]) continue;     //에지는 중복점이 아닌 경우만(점을 비교해야 함)
            bool onHull = true;
            for (int k = 0; k < pts.size(); k++) {
                if (pts[k] == pts[i] || pts[k] == pts[j]) continue;
                if (ccw(pts[i], pts[j], pts[k]) < 0) {  // cw;
                    onHull = false;                     // (i,j) is not an edge;
                    break ;
                }
            }
            if (onHull)  //(i->j) edge is on the hull;
                edges.push_back(std::make_pair(i, j));
        }
    }
    if (edges.size() < 1) return std::vector<CPoint> ();
    // hull을 구성하는 에지정보에서 단순폴리곤 만들기(bug 수정);
    std::vector<CPoint> hull; hull.reserve(edges.size());
    int currIdx = 0;
    hull.push_back(pts[edges[currIdx].first]);
    hull.push_back(pts[edges[currIdx].second]);
    while (edges[currIdx].second != edges[0].first) {
        for (int j = edges.size(); j-->0;) 
            if (edges[j].first == edges[currIdx].second) {
                currIdx = j;
                hull.push_back(pts[edges[currIdx].second]);
                break;
            }
        if (hull.size()==edges.size()) break; //마지막==처음 중복을 피하기 위해
    }
    return hull;
};

convex hull의 edge가 중간에 (collinear) 점을 포함하지 않도록 하기 위해서는, ccw == 0일 때 ABC가 접혀있는지를 체크하면 된다.

주어진 점집합에서 세 점을 뽑아서 만든 삼각형의 외접원에 다른 점이 하나도 포함하지 않으면 triangulation의 기본 삼각형 cell이 된다. 주어진 점으로 만들 수 있는 삼각형의 총개수가 ${}_nC_3$ 이므로, 기본 삼각형을 찾기 위해서는 이들 각각의 삼각형에 대서 나머지 점을 가지고 incircle 테스트를 수행해야 한다. 따라서 이 알고리즘은 ${\cal O}(n^4)$의 스텝이 필요하게 된다.

/*brute force attack*/
foreach point p1
    foreach point p2 
        foreach point p3
            foreach point p4 
                if(incircle(p1,p2,p3,p4))
                    iscell=false;
                    break ;
            endfor;
            if(iscell) 
                 add(triangle(p1,p2,p3));
        endfor;
    endfor;
endfor;

세 점에 의해서 형성이 되는 외접원은 대수적으로 쉽게 구할 수 있다. 여기서는 좀 더 기하학적인 접근을 쓰면, 평면의 점은 

$$(x, y)\rightarrow (x, y, z=x^2 + y^2)$$

의 mapping에 의해서 3차원 paraboloid 곡면의 점으로 옮길 수 있다. paraboloid 위의 세 점이 형성하는 3차원에서 평면이 paraboloid를 절단하는 곡선을 $x-y$ 평면으로 정사영하면 원이 된다는 것을 쉽게 알 수 있다.(incircle 포스팅 참조). 따라서 주어진 점이 세 점의 외접원에 포함되는가를 테스트하는 작업은 이 점을 paraboloid로 올렸을 때의 점과 (paraboloid로 올려진) 외접원의 3점이 형성하는 3차에서의 평면과 관계를 조사하는 것으로 바꿀 수 있다.

주어진 점이 외접원에 포함되면 paraboloid로 변환된 점은 평면의 아래에 놓이고, 외접원 밖의 점이면 평면 위에 놓이게 된다. 물론 외접원 위의 점은 평면에 놓인다. 따라서 평면의 법선 벡터를 구하고, 삼각형의 한 꼭짓점을 기준한 주어진 점의 변위 벡터와 내적을 구하면 내적의 값은 평면 위인지, 아래인지 또는 평면에 놓인 점인가에 따라서 부호가 달라진다. 평면의 수직 벡터를 고정하면(예제는 아래 방향: $n_z < 0$), 평면 위에 놓인 점과의 내적은 음수, 평면 아래에 놓인 점과의 내적은 양수가 되고, 평면의 점과의 내적은 0이다. 

주어진 세 점이 만드는 외접원 내부(and 경계)에 들어가는 점이 없으면 이 삼각형을 선택한다.

** 참고 : Computational Geometry in C(2nd Edition) by Joseph O'Rourke

std::vector<Triple> dt4(const std::vector<double>& x, const std::vector<double>& y) {
    const int n = x.size();
    if (n < 3) return std::vector<Triple> (); // null_vec;
    std::vector<double> z(n);
    for (int i = 0; i < n; i++) 
        z[i] = x[i] * x[i] + y[i] * y[i] ;

    std::vector<Triple> triples;
    /* For each triple (i,j,k) */
    for (int i = 0; i < n - 2; i++ )
        for (int j = i + 1; j < n; j++ )
            for (int k = i + 1; k < n; k++ )
                if ( j != k ) {
                    /* Compute normal to triangle (i,j,k)::  outter_product(j-i, k-i)*/
                    double nx = (y[j] - y[i]) * (z[k] - z[i]) - (y[k] - y[i]) * (z[j] - z[i]); 
                    double ny = (x[k] - x[i]) * (z[j] - z[i]) - (x[j] - x[i]) * (z[k] - z[i]);
                    double nz = (x[j] - x[i]) * (y[k] - y[i]) - (x[k] - x[i]) * (y[j] - y[i]);
                    
                    /* Only examine faces on bottom of paraboloid: nz < 0. */
                    int flag = (nz < 0);
                    if (flag) {
                        /* For each other point m */
                        for (int m = 0; m < n; m++) {
                            /* Check if m above (i,j,k)::i점을 기준으로 m 과 
                            ** normal 간의 내적으로 체크(내적이 양수이면 
                            ** m이 원의 내부에 완전히 들어 있는 경우가 된다. 
                            ** 0인 경우는 원주상에 놓인 경우이므로 배제한다
                            */
                            flag &= ((x[m]-x[i])*nx + (y[m]-y[i])*ny + (z[m]-z[i])*nz <= 0);
                        }
                    }
                    if (flag) {
                        // (i, j, k)의 외접원이 다른 점을 포함하지 않으므로 이 삼각형은 
                        // 삼각분할의 한 면을 형성하게 된다.
                        triples.push_back(Triple(i, j, k));
                    }
                }
    return triples;
}