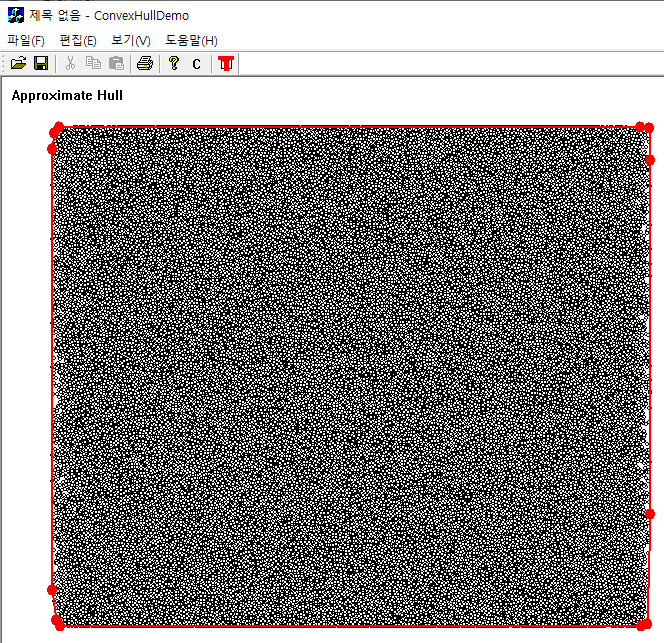
주어진 점집합의 Convex hull을 찾는 알고리즘은 보통 $n \log(n)$ 정도의 time complexity를 가지고 있다. 그러나 점집합의 사이즈가 매우 커지는 경우에는 degeneracy로 인해 optimal한 알고리즘을 사용할 때 매우 주의를 기울려야 한다. 영상처리에서 convex hull을 사용할 때 근사적인 알고리즘만 있어도 충분한 경우가 많이 있는데 이런 경우에 이용할 수 있도록 알고리즘을 수정하자. Convex hull을 만들기 위해서는 점집한을 일정한 순서로 정렬을 하는 과정이 있는데 이 과정이 알고리즘의 가장 복잡한 부분이기도 하다. 이 정렬 과정을 근사적으로 수행하기 위해서 점집합을 수평(또는 수직)으로 일정한 간격으로 나누어진 구간으로 분류를 하자. 이 과정은 주어진 점집합을 한 번 순환만 하면 완료된다. 그런 다음 각 구간에서 수직방향으로(처음 수직방향으로 구간을 나누었으면 수평방향) 가장 바깥에 있는 두 점을 그 구간의 대표점으로 잡아 convex hull을 구하면 원 집합의 근사적인 convex hull이 된다. 이 구간 대표점들은 이미 정렬이 되어 있으므로 대표점 수(~구간 수)에 비례하는 시간 복잡도 이내에 알고리즘이 수행된다. 그리고 구간의 수를 점점 늘릴수록 정확한 convex hull에 근접하게 된다. 아래 그림은 500,000개 점의 근사적인 convex hull을 보여준다(bins=128)
// cross(P1-P0, P2-P0);
// = := colinear;
// < := <p0,p1,p2> CW order;
// > := <p0,p1,p2> CCW order;
static
int ccw(const CPoint &P0, const CPoint &P1, const CPoint &P2 ) {
return (P1.x - P0.x)*(P2.y - P0.y) - (P2.x - P0.x)*(P1.y - P0.y);
}
std::vector<CPoint> approximateHull(const std::vector<CPoint>& Q, int bins) {
if (Q.size() < 3) return std::vector<CPoint> ();
if (bins < 0) bins = max(1, Q.size()/10);
int Lmin = 0, Lmax = 0, Rmin = 0, Rmax = 0;
int left = Q[0].x, right = left;
for (int i = 1; i < Q.size(); i++) {
if (Q[i].x <= left) {
if (Q[i].x < left) {
Lmin = Lmax = i;
left = Q[i].x;
}
else
if (Q[i].y < Q[Lmin].y) Lmin = i;
else if (Q[i].y > Q[Lmax].y) Lmax = i;
}
if (Q[i].x >= right) {
if (Q[i].x > right) {
Rmin = Rmax = i;
right = Q[i].x;
}
else
if (Q[i].y < Q[Rmin].y) Rmin = i;
else if (Q[i].y > Q[Rmax].y) Rmax = i;
}
}
if (left == right) return std::vector<CPoint> (); //vertical line;
//
std::vector<int> slotYhigh(bins + 2, -1);
std::vector<int> slotYlow(bins + 2, -1);
slotYlow.front() = Lmin;
slotYhigh.front() = Lmax;
slotYlow.back() = Rmin;
slotYhigh.back() = Rmax;
//
const CPoint &A = Q[Lmin];
const CPoint &B = Q[Rmin];
const CPoint &C = Q[Lmax];
const CPoint &D = Q[Rmax];
for (int i = 0; i < Q.size(); i++) {
if (Q[i].x == right || Q[i].x == left) continue;
if (ccw(A, B, Q[i]) < 0) { // below line(A,B);
int b = 1 + (bins * (Q[i].x - left)) / (right - left);
if (slotYlow[b]==-1) slotYlow[b] = i;
else if (Q[i].y < Q[slotYlow[b]].y) slotYlow[b] = i;
continue ;
}
if (ccw(C, D, Q[i]) > 0) {// above line(C,D);
int b = 1 + (bins * (Q[i].x - left)) / (right - left);
if (slotYhigh[b]==-1) slotYhigh[b] = i;
else if (Q[i].y > Q[slotYhigh[b]].y) slotYhigh[b] = i;
continue;
}
}
std::vector<CPoint> hull(Q.size());
int s = -1;
for (int i = 0; i <= bins + 1; i++) {
if (slotYlow[i]==-1) continue;
while (s > 0)
if (ccw(hull[s-1], hull[s], Q[slotYlow[i]]) > 0) break;
else s--;
hull[++s] = Q[slotYlow[i]];
};
if (Rmax != Rmin) hull[++s] = Q[Rmax];
//
int s0 = s ;
for (int i = bins; i >= 0; i--) {
if (slotYhigh[i]==-1) continue;
while (s > s0)
if (ccw(hull[s-1], hull[s], Q[slotYhigh[i]]) > 0) break;
else s--;
hull[++s] = Q[slotYhigh[i]];
}
if (hull[s] == hull[0]) s--;
hull.resize(s+1);
return hull;
}728x90
'Computational Geometry' 카테고리의 다른 글
| Alpha Shape (1) | 2024.07.14 |
|---|---|
| Smoothing Spline (0) | 2024.06.29 |
| Catmull-Rom Spline (2) (0) | 2024.06.21 |
| Minimum Volume Box (0) | 2024.06.16 |
| Natural Cubic Spline: revisited (0) | 2024.06.14 |




