Geometry & Recognition

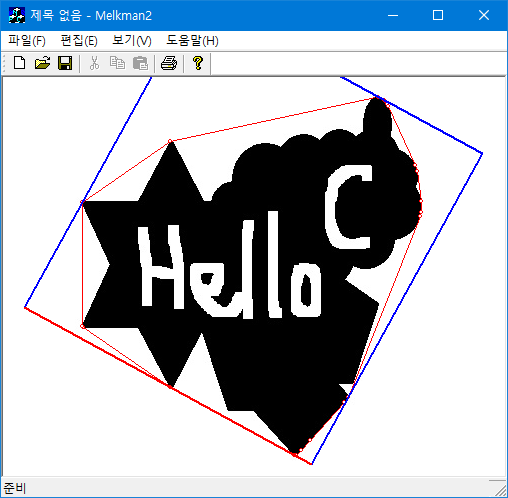
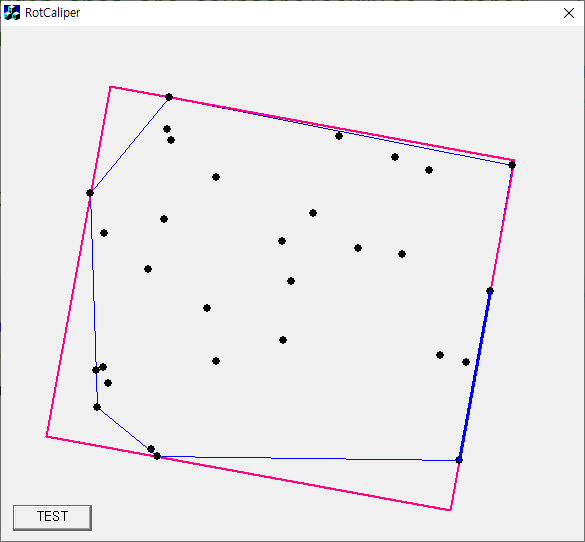
주어진 점들을 감싸는 최소  면적의 직사각형은 먼저 convex hull을 구한 후 rotating caliper을 써서 구할 수 있다. 다음 코드는 반시계방향으로 정렬된 convex hull을 이용해서 minimum volume box을 구한다. 처음 좌표축 방향으로 정렬된 bounding box을 이용해서 가장 작은 각을 형성하는 convex hull의 한 변을 찾고, 그 변으로 만들어지는 bounding box를 구한다. 반시계방향으로 bounding box가 convex hull의 변을 순차적으로 접하도록 회전시키면서 최소 면적인 경우를 찾으면 된다. 이는 convex hull을 바닥에서 굴리면서 bounding box을 찾는 경우로 생각해 보면 더 쉽다. bounding box가 convex hull의 모든 변을 다 순회하면 알고리즘이 종료되므로  time complexity는 $O(N)$이다.

void MinVolumeBox(const std::vector<CfPt>& chull, CfPt mvbox[4]) {
    if (chull.size() < 3) return;
    std::vector<CfPt> edges(chull.size());
    std::vector<int>  visited(chull.size(), 0);  // initialized = 0;
    enum {BB_NONE, BB_LEFT, BB_RIGHT, BB_BOTTOM, BB_TOP};
    for (int i = 0; i < chull.size(); i++) {
        const CfPt e = chull[(i+1) % chull.size()] - chull[i];
        edges[i] = e / e.Norm();// make a unit vector;
    }
    // 먼저 좌표의 최소-최대 값을 구한다;
    // index을 순환할 때, 항상 최대-최소가 (index+chull.size)%chull.size가 되게
    double xmin = chull[0].x, xmax = xmin;
    double ymin = chull[0].y, ymax = curr;
    int left = 0, bot = 0, right = 0, top = 0 ;
    for (int i = 1; i < chull.size(); i++) {
        if (chull[i].x <= xmin)      { xmin = chull[i].x; left = i;}
        else if (chull[i].x >= xmax) { xmax = chull[i].x; right = i;}
        if (chull[i].y <= ymin)      { ymin = chull[i].y; bot = i;}
        else if (chull[i].y >= ymax) { ymax = chull[i].y; top = i;}
    }
    if (chull[0].x <= xmin)       { xmin = chull[0].x; left = 0;}
    else if ( chull[0].x >= xmax) { xmax = chull[0].x; right = 0;}
    if (chull[0].y <= ymin)       { ymin = chull[0].y; bot = 0;}
    else if (chull[0].y >= ymax)  { ymax = chull[0].y; top = 0;}

    /*____Initial mvbox Setting____*/
    CfPt center = CfPt(xmin + xmax, ymin + ymax)/2;
    CfPt ax0 = CfPt(1,0), ax1 = CfPt(0,1);	// mvbox의 unit vectors;
    CfPt eh = ax0, ev = ax1;				// working unit vectors;
    double hscale  = (xmax - xmin) / 2; 
    double vscale  = (ymax - ymin) / 2;
    double minarea = hscale * vscale;		// area / 4;
    int done = 0;
    while (!done) {
        // edges[bot]는 chull[bot+1]-chull[bot];
        // edges[bot],edges[right],edges[top],edges[left] 중에서
        // 현재의 mvbox의 변(eh, ev,-eh,-ev)과 가장 작은 각(max_cosine)을 이루는 
        // edge를 찾음;
        int iflag = BB_NONE;
        double	max_cosine = 0;
        double	cosine = eh * edges[bot];
        if (cosine > max_cosine) { max_cosine = cosine; iflag = BB_BOTTOM;}

        cosine = ev * edges[right]; ;
        if (cosine > max_cosine) { max_cosine = cosine; iflag = BB_RIGHT;}
        
        cosine = -eh * edges[top]; 
        if (cosine > max_cosine) { max_cosine = cosine; iflag = BB_TOP;}
        
        cosine = -ev * edges[left]; 
        if (cosine > max_cosine) { max_cosine = cosine; iflag = BB_LEFT;}
        
        switch (iflag) {
        case BB_BOTTOM:
            if (!visited[bot]) {// edges[bot]가 mvbox의 한변에 포함됨;
                eh = edges[bot]; ev = eh.Rot90(); 
                // 다음 변으로 회전;
                visited[bot] = 1;
                if (++bot == chull.size()) bot = 0;
            } else done = 1;
            break;
        case BB_RIGHT:
            if (!visited[right]) {// edges[right]가 mvbox의 한변에 포함됨;
                ev = edges[right]; eh = -ev.Rot90(); 
                // 다음 변으로 회전;
                visited[right] = 1;
                if (++right == chull.size()) right = 0;
            } else done = 1;
            break;
        case BB_TOP:
            if (!visited[top]) { // edges[top]이 mvbox의 한변에 포함됨;
                eh = -edges[top]; ev = eh.Rot90(); 
                // 다음 변으로 회전;
                visited[top] = 1;
                if (++top == chull.size()) top = 0;
            } else done = 1;
            break;
        case BB_LEFT:
            if (!visited[left]) {// edges[left]가 mvbox의 한변에 포함됨;
                ev = -edges[left]; eh = -ev.Rot90(); 
                // 다음 변으로 회전;
                visited[left] = 1;
                if (++left == chull.size()) left = 0;
            } else done = 1;
            break;
        case BB_NONE: // polygon이 직사각형임;
            done = 1;
            break;
        }
        // check area of mvbox;
        double len0 = eh * (chull[right] - chull[left]) / 2;
        double len1 = ev * (chull[top] - chull[bot]) / 2;
        double area = len0 * len1; //면적의 1/4 임;
        if (area < minarea) {
            minarea	= area;
            ax0	= eh; ax1 = ev;
            hscale = len0; vscale = len1;
            // box center: tt = left 기준 top-bot을 연결하는 vector/2;
            CfPt tt = (chull[top] + chull[bot]) / 2 - chull[left];
            double zz = ev * tt; 
            center = eh * len0 + ev * zz + chull[left];
        }
    }
    eh = ax0 * hscale; // recover original scale;
    ev = ax1 * vscale; // recover original scale;
    mvbox[0] = center + eh + ev;
    mvbox[1] = center - eh + ev;
    mvbox[2] = center - eh - ev;
    mvbox[3] = center + eh - ev;
}

주어진 점집합을 포함하는 최소 면적의 rectangle을 찾는 문제는 점집합의 convex hull을 포함하는 rectangle을 찾는 문제와 같다. convex hull의 한 변을 공유하면서 전체를 포함하는 rectangle 중 최소 면적인 것을 찾으면 된다. Rotating Caliper를 쓰면 $O(n)$ step이 요구된다.

// 방향이 dir이고 A점을 통과하는 직선과 방향이 dir에 수직이고 B점을 통과하는 직선의 교점을 반환;
CPoint LineIntersect(CPoint A, CPoint dir, CPoint B);
//
#define DOT(A,B) ((A).x*(B).x + (A).y*(B).y))
void BoundingRect(std::vector<CPoint>& hull, CPoint vtx[4]) {//non-optimal.
    if (hull.size() < 3) return;
    double minArea = DBL_MAX;
    int bIndex = 0, tIndex = 0, lIndex = 0, rIndex = 0;
    for (int j = 0, i = hull.size() - 1; j < hull.size(); i = j++) {
        CPoint &A = hull[i], &B = hull[j];
        CPoint BA = B - A;  // convex hull의 한 기준변;
        CPoint BAnormal = CPoint(-BA.y, BA.x); //(B-A)에 반시계방향으로 수직인 벡터;
        double BAsq = DOT(BA, BA);
        //기준변과 대척점(antipodal point)을 찾는다: BAnormal방향으로 가장 멀리 떨어진 점
        int id = FindAntipodal(BAnormal, hull) ;
        CPoint QA = hull[id] - hull[i];
        //기준변과 대척점을 통과하는 직선과의 사이거리;
        double D1 = fabs(double(DOT(BAnormal, QA))) / sqrt(BAsq);
        //left_side_end_point;//기준변 반대방향으로 가장 멀리 떨어진 꼭지점;
        int id1 = FindAntipodal(-BA, hull);
        //right_side_end_point;//기준변 방향으로 가장 멀리 떨어진 꼭지점;
        int id2 = FindAntipodal(BA, hull);

        ///가장 왼쪽과 가장 오른쪽 꼭지점을 연결하는 선분
        CPoint H = hull[id1] - hull[id2];  
        //기준변 방향으로 정사영하면 두 평행선 사이거리를 줌;
        double D2 = fabs(double(DOT(BA,H))) / sqrt(BAsq);
        double area = D1 * D2; 
        if (area < minArea) {
            minArea = area;
            bIndex = i ;  tIndex = id;
            lIndex = id1; rIndex = id2;
        }
    }
    //directional vector for base_edge;
    CPoint dir = hull[(bIndex + 1) % hull.size()] - hull[bIndex] ; 
    vtx[0] = LineIntersect(hull[bIndex], dir, hull[lIndex]);
    vtx[1] = LineIntersect(hull[tIndex], dir, hull[lIndex]);
    vtx[2] = LineIntersect(hull[tIndex], dir, hull[rIndex]);
    vtx[3] = LineIntersect(hull[bIndex], dir, hull[rIndex]);
}

https://kipl.tistory.com/606