Geometry & Recognition

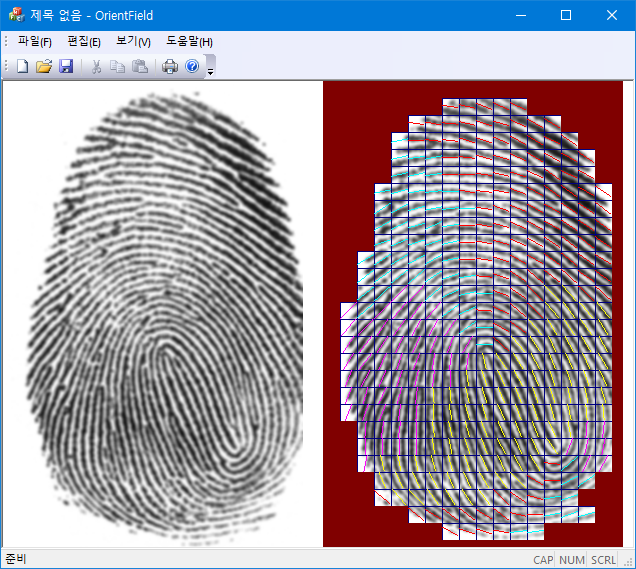
평면에서 주어진 벡터장의 orientation을 찾는 문제는 영상처리 알고리즘에서 자주 접하게 된다. 벡터의 방향은 두 성분의 부호와 상대적인 크기에 따라 달라지지만, 기준선에 대해 상대적으로 기울어진 정도를 나타내는 orientation은 정반대 방향의 두 벡터 $(v_x, v_y)$와 $(-v_x, -v_y)$에 같은 값이 부여되고, 그 값은 벡터의 $x$ 성분과 $y$ 성분의 비의 arctangent 값

$$\theta=\tan^{-1} \left( \frac {v_y}{ v_x }\right)$$

로 계산할 수 있다. 

영상처리에서는 영상에 내재하는 잡음에 의한 영향을 줄이기 위해 한 지점에서 orientation을 추정할 때 보통 그 지점 주변의 벡터 성분의 평균을 이용한다. 주변에서 정반대 방향의 두 벡터가 있는 경우 이 두 벡터는 기하학적으로 같은 orientation을 주지만 더하는 경우 서로 상쇄되어 평균에는 기여가 없으므로 위 식을 사용하면 잘못된 예측을 줄 수 있다. 따라서 잡음을 고려한 상황에서 좀 더 robust 하게 orientation을 추정할 수 있는 방법이 있어야 한다. 벡터 성분의 상대적인 부호만 고려하는 식으로 바꾸기 위해서 $\tan \theta$ 대신에 $\tan (2\theta)$를 고려하자.

\[ \tan (2\theta) = \frac {2\tan(\theta)}{1-\tan^2(\theta)}=\frac {2v_x v_y}{v_x^2 - v_y^2}. \]

분모에서는 각 성분의 제곱, 분자는 두 성분의 곱으로 표현되므로 성분 사이의 상대부호가 같은 경우에는 우측식은 같은 값을 주므로 분모, 분자를 주변 평균값 $v_x v_y ~\longrightarrow ~<v_x v_y>$, $v_x^2 - v_y^2 ~\longrightarrow ~<v_x^2> - < v_y^2>$으로 대체하여도 올바른 orientation을 주게 된다. orientation 각도는

\[ \theta = \frac {1}{2} \tan^{-1}\left( \frac {2 <v_x v_y>}{ <v_x^2> - <v_y^2>}  \right)  \]

으로 주어진다. 실제 계산은 인자가 singular해지는 경우를 피하기 위해서 $\text {atan2}()$ 함수를 사용한다.

https://kipl.tistory.com/293

https://kipl.tistory.com/111

https://kipl.tistory.com/58

지문에서 ridge의 방향(orientation)은 gradient에 수직한 방향이다(그런데 벡터인 gradient와는 달리 ridge의 방향은 모호함이 있다. 시계방향 또는 반시계방향으로 90도 회전이 모두 동일한 ridge의 방향이다).  gradient의 방향각이 $\alpha$일 때 수직인 ridge의 방향각은 $\theta =\frac{\pi}{2} + \alpha$로 정의하자. 방향각을 주어진 gradient 성분 $\nabla I = (g_x, g_y)$로 표현하기 위해서

$$ \sin 2\alpha = 2 \sin \alpha \cos \alpha = 2 \frac{g_x}{\sqrt{g_x^2 + g_y^2}}\frac{g_y}{\sqrt{g_x^2 + g_y^2}}$$

$$\cos 2\alpha = \cos^2 \alpha - \sin^2\alpha = \frac{g_x^2}{g_x^2 + g_y^2} -\frac{g_y^2}{g_x^2 +g_y^2}$$ 

임을 이용하자. $$\tan 2\alpha = \frac{ 2g_x g_y}{ g_x^2 - g_y^2}$$로 쓸 수 있으므로 ridge의 방향각은

$$ \theta =\frac{\pi}{2} + \frac{1}{2} \arctan \frac{2g_x g_y}{g_x^2 - g_y^2}$$

임을 알 수 있다. $(g_x, g_y) \rightarrow (-g_x, -g_y)$이더라도 ridge의 방향은 동일하므로 $\theta$의 범위는 $0\le \theta < \pi$로 제한된다.

이미지의 한 지점에서 ridge의 방향은 그 점을 중심으로 하는 적당한 크기의 윈도 평균값으로 추정한다. gradient 성분은 Sobel 연산자나 Prewitt 연산자를 convolution해서 얻을 수 있다. 따라서 지문 이미지 상의 픽셀 좌표 $(i,j)$에서 ridge의 방향은

$$\theta_{ij} = \frac{\pi}{2} +\frac{1}{2}\arctan \frac{2 G_{xy}}{G_{xx} - G_{yy}}$$

$$ G_{xy} = \sum_{W} \text{gradX}_{ij} \times \text{gradY}_{ij}$$

$$ G_{xx} = \sum_{W} \text{gradX}_{ij} \times \text{gradX}_{ij}$$

$$ G_{yy} = \sum_{W} \text{gradY}_{ij} \times \text{gradY}_{ij}$$

아래 결과는 5x5 크기의 Gaussian filter를 적용한 지문 이미지에 17x17 크기의 윈도를 겹치지 않게 잡아서 평균을 계산한 결과다. $G_{xx}+G_{yy}$가 최대값의 $20\%$보다 작은 영역은 방향을 표시하지 않았다 (red:0~45, yellow:45~90, magenta: 90~135, cyan: 135~180).

int RidgeOrientaion(BYTE *img, int w, int h, int bsz/*17*/, double *omap) {
    const int nn[] = {-w - 1, -w, -w + 1, -1, 0, 1, w - 1, w, w + 1};
    const int sobelX[] = {-1, 0, 1, -2, 0, 2, -1, 0, 1};
    const int sobelY[] = {-1, -2, -1, 0, 0, 0, 1, 2, 1};
    const int xmax = w - 1, ymax = h - 1;
    std::vector<int> gradx(w * h, 0);
    std::vector<int> grady(w * h, 0);
    for (int y = 1, pos = w; y < ymax; y++) {
        pos++; //x = 0;
        for (int x = 1; x < xmax; x++, pos++) {
            int sx = 0, sy = 0; 
            for (int k = 0; k < 9; k++) {
                int v = img[pos + nn[k]];
                sx += sobelX[k] * v;
                sy += sobelY[k] * v;
            }
            gradx[pos] = sx;
            grady[pos] = sy;
        }
        pos++; // x = xmax;
    }
    const int ny = h / bsz;
    const int nx = w / bsz;
    for (int iy = 0; iy < ny; iy++) {
        for (int ix = 0; ix < nx; ix++) {
            int sxy = 0, sxx = 0, syy = 0; 
            int pos = (iy * w + ix) * bsz; //starting position of block(ix, iy)
            int *dx = &gradx[pos];
            int *dy = &grady[pos];
            for (int jj = 0; jj < bsz; jj++) {
                for (int ii = 0; ii < bsz; ii++) {
                    int gx = dx[jj * w + ii];
                    int gy = dy[jj * w + ii];
                    sxy += gx * gy;
                    sxx += gx * gx;
                    syy += gy * gy;
                }
            }
            omap[iy * nx + ix] = 0.5 * (PI + atan2(double(2.0 * sxy), double(sxx - syy)));
        }
    }
    //...identify fingerprint regions and draw orientation map;
    return 1;
}