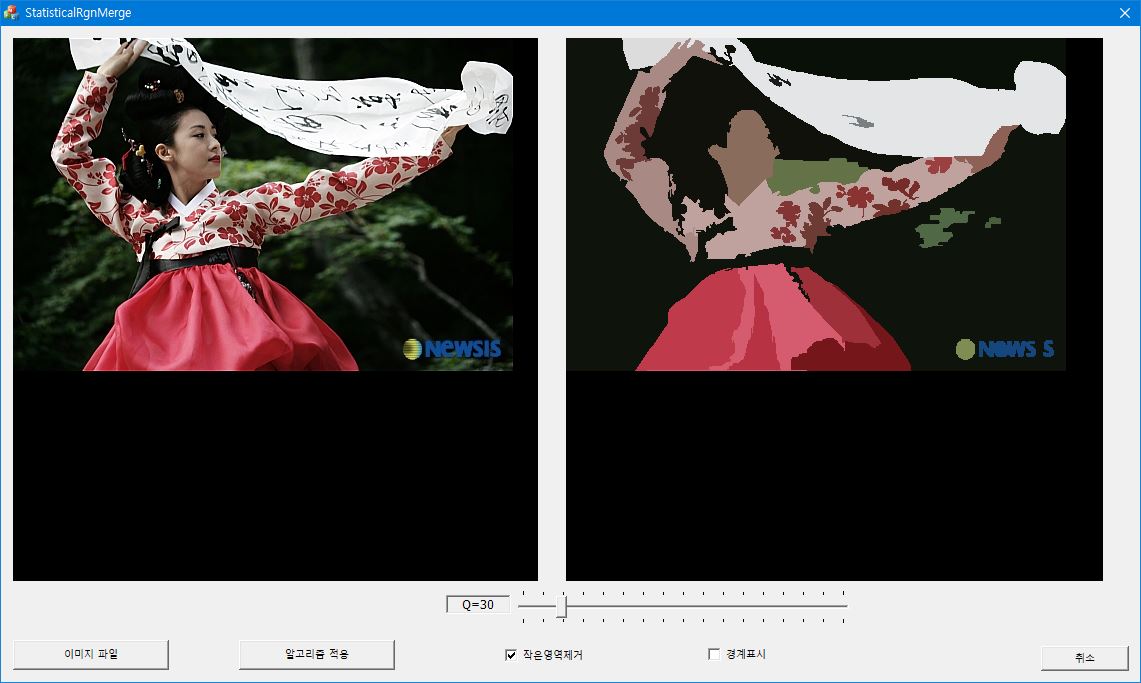
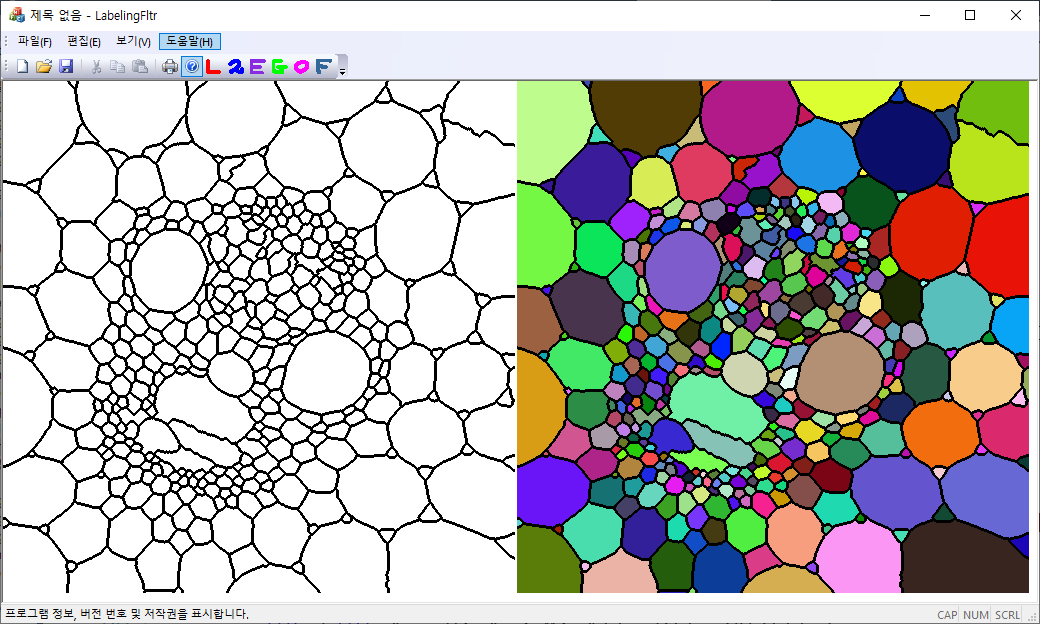
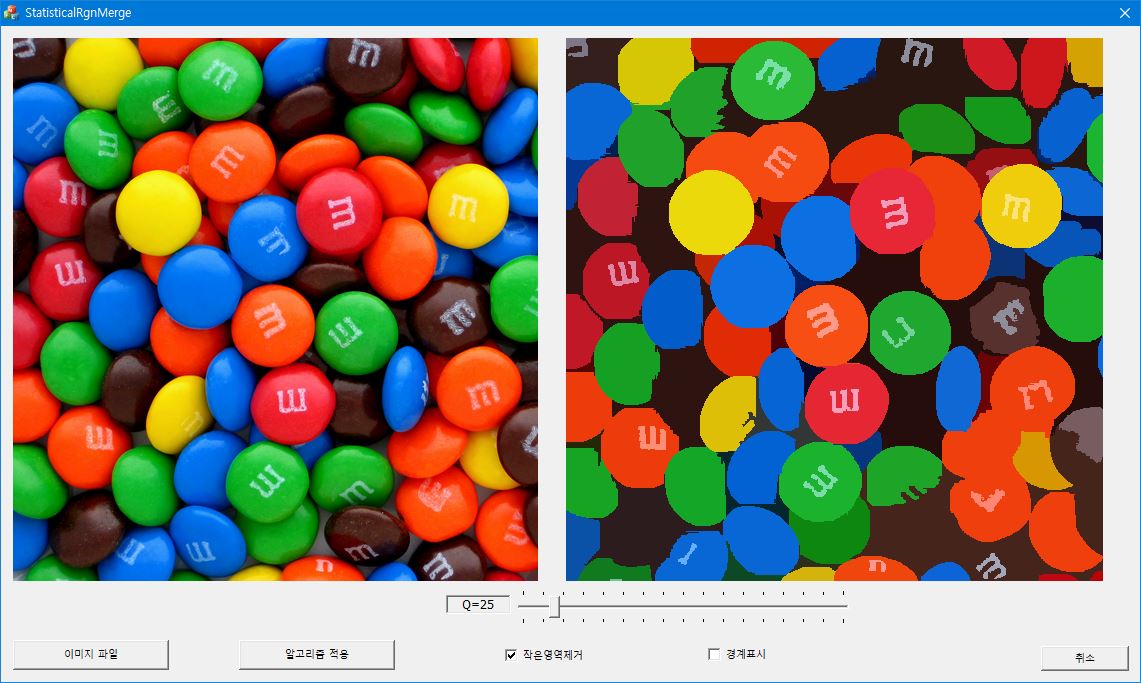
Statistical region merging은 이미지의 픽셀을 일정한 기준에 따라 더 큰 영역으로 합병하는 bottom-up 방식의 과정이다. 두 영역 $R_1$과 $R_2$가 하나의 영역으로 합병이 되기 위해서는 두 영역의 평균 픽셀 값의 차이가
$$ g \sqrt{ \frac {\ln(2/\delta)}{2Q} \Big( \frac {1}{|R_1|}+ \frac {1}{|R_2|}\Big) }$$
를 넘지 않아야 한다. $g=256$으로 gray 레벨의 갯수를 의미하고, $|R_i|$는 $R_i$ 영역에 포함된 픽셀 수를 나타낸다. $\delta$는 작은 수로 이미지의 픽셀 수의 제곱에 반비례한다. 보통 $\delta = 1/(6\times \text {width}\times \text {height})^2$로 선택한다. $Q$는 이미지의 통계적인 복잡성을 정량화하는 양으로 이 알고리즘에서는 외부에서 설정이 되는 값이다. 낮은 $Q$값을 선택하면 분할된 영역의 수가 작아지고(undersegmentation), 반대로 높은 $Q$ 값을 입력하면 분할된 영상에 너무 많은 영역이 나타나게 된다(oversegmentation).
Ref:
https://en.wikipedia.org/wiki/Statistical_region_merging
http://www.lix.polytechnique.fr/~nielsen/Srmjava.java
Srm::Srm(int width, int height, BYTE *image) {
this->width = width;
this->height = height;
int n = width * height;
this->count = new int [n];
this->Ravg = new float [n];
this->Gavg = new float [n];
this->Bavg = new float [n];
this->image = image;
// disjoint sets with n pixels;
this->UF = new Universe(n);
// initialize to each pixel a leaf region;
for (int i = 0, pos = 0; i < n; i++, pos += 3) {
count[i] = 1;
Bavg[i] = image[pos ];
Gavg[i] = image[pos + 1];
Ravg[i] = image[pos + 2];
}
this->Q = 32; // adjustable.
this->g = 256.0;
this->logDelta = 2. * log(6.0 * n);
}
bool Srm::Predicate(int rgn1, int rgn2) {
double dR = (Ravg[rgn1] - Ravg[rgn2]); dR *= dR;
double dG = (Gavg[rgn1] - Gavg[rgn2]); dG *= dG;
double dB = (Bavg[rgn1] - Bavg[rgn2]); dB *= dB;
double logreg1 = min(g, count[rgn1]) * log(1.0 + count[rgn1]);
double logreg2 = min(g, count[rgn2]) * log(1.0 + count[rgn2]);
double factor = g * g / (2.0 * Q);
double dev1 = factor * (logreg1 + logDelta) / count[rgn1] ;
double dev2 = factor * (logreg2 + logDelta) / count[rgn2] ;
double dev = dev1 + dev2;
return ( (dR < dev) && (dG < dev) && (dB < dev) );
}
void Srm::Merge(int rgn1, int rgn2) {
if (rgn1 == root2) return;
int w1 = count[rgn1], w2 = count[rgn2];
int root = UF->Union(rgn1, rgn2);
//update the merged region;
count[root] = w1 + w2;
double count_sum = w1 + w2;
Ravg[root] = (w1 * Ravg[rgn1] + w2 * Ravg[rgn2]) / count_sum;
Gavg[root] = (w1 * Gavg[rgn1] + w2 * Gavg[rgn2]) / count_sum;
Bavg[root] = (w1 * Bavg[rgn1] + w2 * Bavg[rgn2]) / count_sum;
}
Edge* Srm::Pairs(int nedge) {
// 4-connectivity;
int ymax = height - 1, xmax = width - 1;
Edge* edgeList = new Edge[nedge];
int cnt = 0;
for (int y = 0; y < ymax; y++) {
for (int x = 0; x < xmax; x++) {
int pos = y * width + x;
int b1 = image[3 * pos + 0];
int g1 = image[3 * pos + 1];
int r1 = image[3 * pos + 2];
//right: x--x
edgeList[cnt].r1 = pos; //current
edgeList[cnt].r2 = pos + 1; //right
int bdiff = abs(b1 - image[3 * (pos + 1) + 0]);
int gdiff = abs(g1 - image[3 * (pos + 1) + 1]);
int rdiff = abs(r1 - image[3 * (pos + 1) + 2]);
edgeList[cnt++].diff = max3(bdiff, gdiff, rdiff) ;
//below: x
// |
// x
edgeList[cnt].r1 = pos;
edgeList[cnt].r2 = pos + width;
bdiff = abs(b1 - image[3 * (pos + width) + 0]);
gdiff = abs(g1 - image[3 * (pos + width) + 1]);
rdiff = abs(r1 - image[3 * (pos + width) + 2]);
edgeList[cnt++].diff = max3(bdiff, gdiff, rdiff);
}
}
//x=width-1;
for (int y = 0; y < ymax; y++) {
int pos = y * width + (width - 1); // (x,y) = (width-1, y)
// x
// |
// x
edgeList[cnt].r1 = pos;
edgeList[cnt].r2 = pos + width;
int bdiff = abs((int)image[3 * pos + 0] - image[3 * (pos + width) + 0]);
int gdiff = abs((int)image[3 * pos + 1] - image[3 * (pos + width) + 1]);
int rdiff = abs((int)image[3 * pos + 2] - image[3 * (pos + width) + 2]);
edgeList[cnt++].diff = max3(bdiff, gdiff, rdiff);
}
//y=height-1;
for (int x = 0; x < xmax; x++) {
int pos = (height - 1) * width + x; //(x,y)=(x, height-1);
//right; x--x
edgeList[cnt].r1 = pos;
edgeList[cnt].r2 = pos + 1;
int bdiff = abs((int)image[3 * pos + 0] - image[3 * (pos + 1) + 0]);
int gdiff = abs((int)image[3 * pos + 1] - image[3 * (pos + 1) + 1]);
int rdiff = abs((int)image[3 * pos + 2] - image[3 * (pos + 1) + 2]);
edgeList[cnt++].diff = max3(bdiff, gdiff, rdiff);
}
return edgeList;
}
int Srm::Segment() {
// 4-connectivity
int nedge = 2 * (width - 1) * (height - 1) + (height - 1) + (width - 1);
Edge* edgeList = Pairs(nedge);
BucketSort(edgeList, nedge);
for (int i = 0; i < nedge; i++) {
Edge &e = edgeList[i];
int r1 = UF->Find(e.r1);
int r2 = UF->Find(e.r2);
if ((r1 != r2) && (Predicate(r1, r2)))
Merge(r1, r2);
}
delete [] edgeList;
int rgn_count = 0;
for (int node = width * height; node-- > 0;)
if (UF->IsRoot(node)) rgn_count++;
return rgn_count;
}
// sorting with buckets; returns an ordered edgeList;
void BucketSort(Edge* &edgeList, int n) {
int hist[256] = {0}, chist[256];
for (int i = 0; i < n; i++) hist[edgeList[i].diff]++;
// cumulative histogram
chist[0] = 0; // Note, chist[0] ne hist[0];
for (int i = 1; i < 256; i++)
chist[i] = chist[i - 1] + hist[i - 1];
Edge *ordered = new Edge [n];
for (int i = 0; i < n; i++)
ordered[chist[pair[i].diff]++] = pair[i];
delete[] edgeList;
edgeList = ordered;
}'Image Recognition > Fundamental' 카테고리의 다른 글
| 영상에 Impulse Noise 넣기 (2) | 2023.02.09 |
|---|---|
| Canny Edge: Non-maximal suppression (0) | 2023.01.11 |
| Moment-preserving Thresholding (0) | 2022.05.29 |
| Minimum Cross Entropy Thresholding (0) | 2022.05.29 |
| Quadtree Segmentation (0) | 2022.05.21 |