$$I=\text{Pr} \int_{0}^{\infty} \frac{x^a}{x+b} dx , \quad - 1 < a <0,\quad b<0$$
복소함수 $f(z)= \frac{z^a}{z+b}$를 그림과 같은 contour $\Gamma=C_\epsilon +C_1 + C_2 +C_3 +C_\infty + C_4 +C_5 +C_6$에 대해서 적분할 것이다. $z=0,\infty$이 branch point이므로 branch cut을 $+x$축으로 선택하고, $z=-b>0$가 simple pole이므로 Cauchy principal value을 구하는 문제이다. 주어진 contour에서 analytic 하므로 $\int_{\Gamma} f(z) dz = 0$.
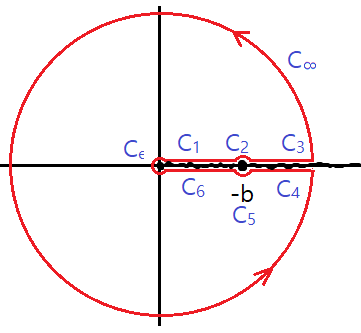
1. $C_\epsilon$:
$$\int_{C_\epsilon} f(z) dz = O( \epsilon^{1+a})\longrightarrow 0.$$
2. $C_1 + C_3$: $z=x e^{i0} ~(x: 0\rightarrow \infty)$,
$$\int_{C_1+C_3} f(z) dz = \text{Pr} \int_0^\infty \frac{(x e^{i0})^a }{x+b} dx = I.$$
3. $C_4 + C_6$: $z= xe^{2\pi i} ~(x: \infty \rightarrow 0)$,
$$\int_{C_4 +C_6} f(z)dz = \text{Pr}\int_\infty ^ {0} \frac{ (x e^{2\pi i})^a }{x + b} dx =- e^{2\pi ai} I .$$
4. $C_2$: $z= (-b) e^{0i}, ~z+b= \epsilon e^{\theta i}~(\theta:\pi \rightarrow 0)$
$$\int_{C_2} f(z)dz = \int_{\pi}^{0} \frac{ (-be^{0i})^a }{\epsilon e^{\theta i} } i\epsilon e^{\theta i} d \theta = -i \pi (-b )^a .$$
5. $C_5$: $z=(-b) e^{2\pi i} ,~ z+b = \epsilon e^{\theta i}, ~(\theta: 2\pi \rightarrow \pi)$,
$$\int_{C_5} f(z) dz =\int_{2\pi}^{\pi} \frac{ (-be^{2pi i})^a }{ \epsilon e^{\theta i}} i \epsilon e^{\theta i} d \theta = -i \pi (-b)^a e^{2\pi a i}.$$
6.$C_\infty $:
$$\int_{C_\infty} f(z) dz= O(R^a) \longrightarrow 0.$$
따라서,
$$\int_{\Gamma} f(z)dz = I (1 - e^{2\pi ai }) - i\pi (-b)^a (1 + e^{2\pi a i}) = 0$$
$$\therefore~ I= \text{Pr}\int_0^\infty \frac{x^a }{x +b} dx = - (-b)^a\pi \cot (\pi a).$$
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-009 (0) | 2021.01.03 |
|---|---|
| Integration along branch cuts-008 (0) | 2021.01.03 |
| Integration along a branch cut-006 (0) | 2020.02.28 |
| 주어진 길이의 폐곡선으로 가둘 수 있는 최대 면적의 도형은? (0) | 2020.02.15 |
| Integration along a branch cut-005 (0) | 2017.07.02 |


























