Interpolation은 이산적으로 주어진 샘플들 사이에서 존재하지 않는 값을 추정하는 작업이다. 한 지점에서 interpolation을 통해 값을 추정하기 위해서는 주변의 알려진 샘플 값들을 참조해야 하고 적절한 가중치를 주어야 한다. 또한 interpolation 함수는 충분히 부드럽게 주변 샘플 값들과 연결이 되어야 한다. 이런 관점에서 보면 interpolation은 주변 샘플에 적절한 가중치를 주는 kernel 함수와 convolution으로 이해할 수 있고, 또한 샘플링 과정에서 잃어버린 정보를 샘플 데이터를 smoothing해서 복원하는 과정으로 해석할 수 있다.
kernel 함수가 $K(x)$고, 일정한 간격으로 주어진 1차원 샘플의 값이 $\{ (x_k, c_k)\}$일 때 interpolation 함수는
$$ f(x) =\sum_k c_k K \Big( \frac{x - x_k}{h}\Big)$$
의 형태로 표현할 수 있다. $h$는 샘플의 간격으로 이미지에서는 픽셀의 간격이므로 $h=1$이다.
interpolation함수는 샘플 위치를 통과해야 하므로,
$$ f(x_j) = c_j = \sum_{k} c_k K( x_j - x_k) \quad \longrightarrow\quad K(x_j - x_k ) = \delta_{jk}$$
즉, $K(0)=1$이고, $K(i)=0~(i\ne 0)$임을 알 수 있다. 또한 kernel이 주는 가중치의 합이 1이어야 하므로
$$\int_{-\infty}^{\infty} K(x) dx = 1$$이어야 한다.
영상처리에서 잘 알려진 interpolation 방법은 nearest-neighbor, linear, cubic interpolation이 많이 사용된다. 아래 그림은 kernel의 중심이 원점에 있는 경우를 그렸다.
Nearest neighbor:
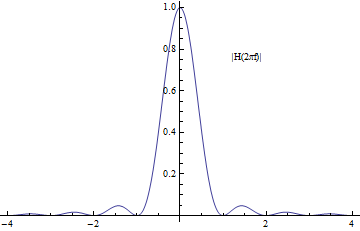
$$ K(x) = \left\{ \begin{array}{ll} 1, & |x| < \frac{1}{2} \\ 0, & |x| \ge\frac{1}{2}\end{array} \right. , \quad\quad H(\omega) =\int_{-\infty}^{\infty} K(x) e^{-i\omega x}dx= \text{sinc} \Big( \frac{\omega}{2} \Big) $$
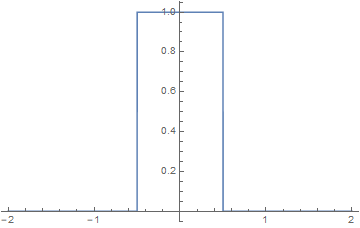

Linear interpolation:
$$ K(x) = \left\{ \begin{array}{ll} 1 - |x| , & |x| < 1 \\ 0, & |x| \ge 1 \end{array} \right. , \quad\quad H(\omega) = \text{sinc}^2 \Big(\frac{\omega}{2} \Big) $$
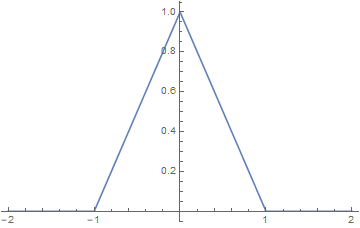
Cubic interpolation:
$$ K(x) = \left\{ \begin{array}{ll} \frac{1}{2}( 3|x|^3 - 5|x|^2 +2) , & |x| < 1 \\ \frac{1}{2}(-|x|^3 +5 |x|^2 -8|x|+4 ) , & 1\le |x| <2 \\ 0 , & |x| \ge 2 \end{array} \right. , \\ \quad\quad H(\omega) = \frac{12}{\omega^2} \Big( \text{sinc}^2 \Big(\frac{\omega}{2}\Big) -\text{sinc}(\omega) \Big) -\frac{4}{ \omega^2} \Big( 2\text{sinc}^2 (\omega) -2 \text{sinc}(\omega) -\text{sinc}(2\omega) \Big) $$

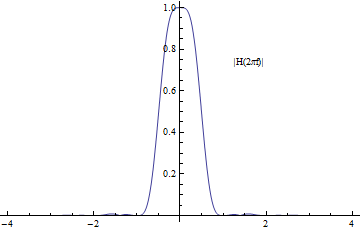
Cubic interpolation kernel이 다른 nearest-neighbor, linear kernel 보다 low-pass 특성이 강해지므로 이미지가 더 잘 smoothing 되는 특성을 가질 것임을 알 수 있다.
double KernelCubic(double x) {
double absx = fabs(x);
if (absx < 1) return 0.5 * (2 + absx * (absx * (3 * absx - 5)))
if (absx < 2) return 0.5 * (4 - absx * (absx * (absx + 5) - 8));
return 0;
}일반적인 cubic convolution kernel은 4개의 샘플데이터를 이용해 보간하므로 폭이 4(반지름 =2)이다. $x_k=-1,0,1,2$에서 4개의 샘플값 $c_0, c_1, c_2,c_3$이 주어진 경우, $0\le x <1$구간에서 cubic interpolation은 kernel의 중심을 원점에서 $x$로 평행이동하면,
$$f(x) = c_0 K(-1-x) + c_1 K(-x) + c_2 K(1-x) + c_3 K(2-x)$$
로 표현된다. 다음 예는 $0\le x<1$ 구간에서 $(x-1)^2$(blue)을 cubic interpolation(red)을 한 결과이다.
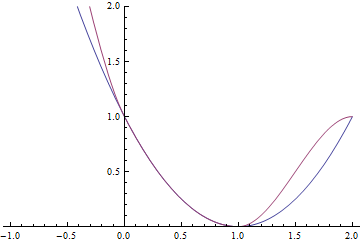
일반적인 cubic convolution kernel은 한 개의 모양을 조정하는 한 개의 조정 parameter을 가지는 연속이고 한 번 미분가능한 형태로 주어진다.
$$ K(x) = \left\{ \begin{array}{ll} (a+2) |x|^3 - (a+3) |x| ^2 +1, & |x| < 1 \\ a|x|^3 - 5a |x|^2 + 8a |x| - 4a ,& 1 \ |x| <2 \\ 0 ,& |x| \ge 2 \end{array} \right. $$
실용적인 파라미터의 범위는 $[-3,0]$이고( $a<-3$이면 $|x|<1$ 구간에서 단조감소가 아니어서 0이 아닌 곳에서 1보다 큰 값을 갖게 된다), 보통 많이 사용하는 cubic interpolation은 $a=-0.5$에 해당한다. 일반적으로 $a$가 -3에 가까워지면 최소 위치가 더 깊어지므로 일종의 미분 연산자처럼 작용하게 되어 이미지에 적용할 때 sharpness가 증가하게 된다. $a$가 0에 가까워지면 최소 위치 깊이가 0에 가까워지므로 gaussian filter처럼 이미지를 blurring하는 효과가 발생한다.

Lanczos Interpolation:
$$K(x) = \left\{ \begin{array}{ll} \text{sinc}(\pi x) \text{sinc}(\pi x / a), & |x|<a \\ 0 ,& |x|\ge a\end{array}\right.$$
$$H(\omega)=\frac{1}{2\pi^2\sqrt{2\pi}}\Big( -(2\pi-3\omega)\text{Si}(2\pi-3\omega)+(4\pi -3\omega)\text{Si}(4\pi-3\omega)\\+(2\pi +3\omega)\text{Si}(2\pi+3\omega)+(4\pi+3\omega)\text{Si}(4\pi+3\omega)\Big)$$

Fixed-Point Bicubic Interpolation
아날로그 신호로부터 디지털 데이터로 바꿀 때 보통 시간당(sound) 또는 공간적 거리당(image) 일정한 횟수로 데이터를 수집한다. 이 비율을 sampling rate이라 한다. 그런데 sampling rate을 바꾸어야 할
kipl.tistory.com
Bicubic Interpolation
이미지 처리에서 픽셀 좌표는 간격이 1인 2차원 그리드의 교차점으로 볼 수 있다. 이미지를 확대하거나 축소할 때, 픽셀과 픽셀 사이 구간에서 값이 필요한 경우가 생긴다. 간단히는 주변의 가장
kipl.tistory.com
'Image Recognition > Fundamental' 카테고리의 다른 글
| Sampling Theorem (0) | 2021.05.12 |
|---|---|
| Lanczos Resampling (0) | 2021.05.08 |
| Fowler Angle (0) | 2021.04.05 |
| Brute-Force Euclidean Distance Transform (0) | 2021.03.14 |
| 이미지에 Poisson Noise 넣기 (0) | 2021.03.06 |




