Tautochrone Curve(등시곡선)

수직 평면 상에서 곡선 $y=y(x)$을 따라 움직이는 물체의 운동을 생각하자. 이 물체는 마찰이 없이 움직일 수 있고 일정한 중력의 영향을 받는다. 높이 $y=h$에서 출발하여 바닥 $y=0$에 도달하는 데 걸리는 시간은 일반적으로 출발 높이에 따라 달라진다. 역학적 에너지 보존법칙을 쓰면 바닥까지 내려오는 데 걸리는 시간 $T(h)$는

$$\frac{1}{2}(\frac{d\ell }{dt}{)}^2+mgy=mgh⟹T(h)=\frac{1}{\sqrt{2g}}{\int }_0^h\frac{d\ell }{\sqrt{h-y}}$$

일반적으로 출발 높이가 낮으면 움직이는 거리가 짧아지므로 도착 시간도 짧아진다. 그러나 가속이 충분히 되지 않으므로 거리에 비례해서 시간이 짧아지지는 않는다. 그럼 도착 시간이 출발 높이에 무관하게 일정한 곡선을 찾을 수 있을까? 물론 답은 있고,  그때 물체가 움직이는 곡선을 tautochrone curve(등시곡선)이라 부른다.

 

물체가 움직이는 경로의 line element $d\ell$를 $$d\ell =\sqrt{d{x}^2+d{y}^2}=\sqrt{1+(\frac{dx}{dy}{)}^2}dy=f(y)dy$$처럼 쓰면 도착 시간은 $$T(h)=\frac{1}{\sqrt{2g}}{\int }_0^h\frac{f(y)}{\sqrt{h-y}}dy$$

가 된다. 이는 $f(y)$와 $1/\sqrt{y}$의 convolution 형태가 되어 Laplace 변환을 사용하기 좋은 모양이다. 양변에 Laplace 변환을 취하면

$$\begin{array}{rl}\tilde{T}(s)& =\frac{1}{\sqrt{2g}}{\int }_0^{\mathrm{\infty }}{\int }_0^h\frac{f(y)}{\sqrt{h-y}}{e}^{-sh}dydh\\ & =\frac{1}{\sqrt{2g}}\tilde{f}(s)\mathcal{L}[\frac{1}{\sqrt{h}}](s)\\ & =\frac{1}{\sqrt{2g}}\tilde{f}(s)\sqrt{\frac{\pi }{s}}\end{array}$$ 여기서  $\mathcal{L}\left[\frac{1}{\sqrt{h}}\right]=\sqrt{\frac{\pi }{s}}$임을 이용했다 $({\int }_0^{\mathrm{\infty }}\frac{e^{-sh}}{\sqrt{h}}dh=2{\int }_0^{\mathrm{\infty }}{e}^{-s{t}^2}dt=\sqrt{\frac{\pi }{s}})$. 

도착 시간이 높이에 무관하게 일정하다면 $$T(h)=T_0=\text{const}$$로 쓸 수 있으므로 Laplace 변환은 $\tilde{T}(s)=T_0/s$이다. 따라서 곡선 형태를 결정하는 $f(y)$의 Laplace 변환은

$$\tilde{f}(s)=\sqrt{\frac{2g{T}_0^2}{{\pi }^2}}\sqrt{\frac{\pi }{s}}$$ 이를 역변환시키면 

$$f(y)=\sqrt{\frac{2g{T}_0^2}{{\pi }^2}}\frac{1}{\sqrt{y}}$$임을 쉽게 알 수 있다. 이제 구체적인 곡선의 형태를 구하면 $$x=\int dx=\int \sqrt{f^2(y)-1}dy=\int \sqrt{\frac{2g{T}_0^2/{\pi }^2-y}{y}}dy$$이고, 적분하기 위해 곡선이 $(x,y)=(0,0)$을 통과하는 조건을 주자. 그리고 $$y=\frac{2g{T}_0^2}{{\pi }^2}{\sin }^2(\theta /2)=\frac{g{T}_0^2}{{\pi }^2}(1-\cos \theta )$$로 매개변수화하면(이 경우 $dy/dx=\tan (\theta /2)$)

$$x={\int }_0^{{\theta }_0}\frac{g{T}_0^2}{{\pi }^2}(1+\cos \theta )d\theta ⟹x=\frac{g{T}_0^2}{{\pi }^2}(\theta +\sin \theta )$$

이어서 $(x(\theta ),y(\theta ))$는 cycloid가 됨을 알 수 있다. 이 cycloid는 반지름 $g{T}_0^2/{\pi }^2$인 원을 일정한 높이의 수평선 $y=2g{T}_0^2/{\pi }^2$에 접하게 굴릴 때 원점에서 바닥과 접촉했던 점이 그리는 곡선이고, $\theta$는 원의 중심과 이 점을 잇는 선분이 수직과 이루는 각을 나타낸다. 

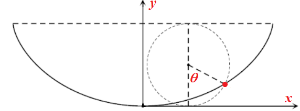
위에서 구한 cycloid 곡선을 도착시간 공식에 대입해서 확인해 보자. 출발 높이가 $h$일 때 $h=\frac{g{T}_0^2}{{\pi }^2}(1-\cos {\theta }_0)$로 놓으면 $$\begin{gathered} h-y=\frac{g{T}_0^2}{{\pi }^2}(\cos \theta -\cos {\theta }_0) \\ d\ell =\frac{g{T}_0^2}{{\pi }^2}\sqrt{2(1+\cos \theta )}d\theta \end{gathered}$$

이므로 내려가는데 걸리는 시간 $$\begin{array}{rl}T(h)& =\frac{T_0}{\pi }{\int }_0^{{\theta }_0}\sqrt{\frac{1+\cos \theta }{\cos \theta -\cos {\theta }_0}}d\theta \\ & =\frac{2T_0}{\pi }{\int }_0^{{\theta }_0}\frac{d\sin (\theta /2)}{\sqrt{{\sin }^2({\theta }_0/2)-{\sin }^2(\theta /2)}}=T_0\end{array}$$이 출발 높이($=h$)에 상관없이 일정함을 확인할 수 있다. 바닥까지 내려가는데 걸리는 시간 $T_0$가 정해지면 원의 반지름 $g{T}_0^2/\pi$이 결정되어 곡선 모양이 자동으로 정해진다.

https://youtu.be/Ib1TdgeYL4o

Cycloid는 이 성질 이외에도 일정한 중력하에서 두 지점을  연결하는 곡선을 움직일 때 최단 시간을 주는 곡선이기도 하다(brachistochrone curve) 

https://kipl.tistory.com/186

등시진자