Geometry & Recognition

함수 $f(x)$의 Fourier transform:

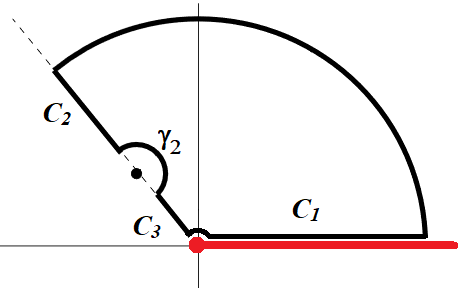
$$ \tilde{f} (k) = \int_{-\infty}^\infty \frac{1}{( i (x- i\epsilon))^\alpha} e^{i k x} dx= |k|^{\alpha-1} {\Gamma(1-\alpha)} \sin(\pi\alpha) (1+ \text{sgn}(k)) $$여기서 $\epsilon \to 0^+$은 미소양수이고, $0<\alpha< 1$는 실수이다. 함수 $$ f(z) = \frac{1}{ (i (z-i\epsilon))^\alpha}$$는 $z=i\epsilon$가 branch point이므로 그림과 같이 cutline을 잡는다: $-\frac{3\pi}{2} \le \arg(z)\le \frac{\pi}{2}$.

$k<0$일 때는 lower half plane을 도는 적분경로를 잡으면 $\tilde{f} =0$임을 보일 수 있고($k<0$에서 0이 아닌 결과를 얻기 위해서는 $x-i\epsilon$를 $x+i \epsilon$으로 치환한다), $k>0$인 경우는 그림과 같이 upper half plane에서 cutline을 감싸는 반원경로에서 적분을 고려하자.

이 경로 내에서 analytic 하므로 $f(z)$의 Fourier transform은 cutline을 감싸는 두 경로 $C_1$과 $C_2$에서 적분으로 표현할 수 있다. Branch point를 감싸는 미소원호에서 적분은 0으로 수렴한다.

경로 $C_1$에서 $$ z= y e^{ i \pi/2} ~(y: \infty\to \epsilon), ~dz= i dy, \\ \int_{C_1} = \int_\infty^\epsilon  e^{- i\pi\alpha/2} e^{-\alpha \log y - i \pi \alpha/2} e^{-ky} (idy)=  -i e^{-i \pi \alpha} \int_0^\infty \frac{e^{-ky}}{y^\alpha} dy$$ 경로 $C_2$에서는 $$ z= y e^{- i 3\pi/2}~(y: \epsilon \to \infty), ~dz=idy \\ \int_{C_2}= \int_\epsilon^\infty e^{-i \pi \alpha /2} e^{- \alpha \log y + i 3\pi\alpha/2} e^{-ky} (idy)= i e^{i \pi\alpha} \int_0^\infty \frac{ e^{-ky}}{ y^\alpha }dy$$ 이 두 경로에서의 적분합은 $$\int_{C_1+C_2} = i (e^{i \pi\alpha}- e^{-i \pi\alpha}) \int_0^ \infty \frac{e^{-ky}}{y^\alpha} dy \\ = - 2\sin(\pi \alpha) \int_0^\infty \frac{e^{-ky}}{y^\alpha} dy = -  2 k^{\alpha-1}{\Gamma(1-\alpha) } \sin (\pi \alpha) \qquad (k>0)$$ 따라서 그림의 경로에서 $f(z)e^{i kz}$가 analytic 하므로 

$$ \oint f(z) e^{ikz} dz = 0 \quad \to \quad \int_{-\infty}^\infty f(x) e^{ikx} dx = -\int_{C_1+C_2} f(z) e^{i kz}dz $$ $k<0$일 때 0임을 고려하면, $$ \int_{-\infty }^\infty \frac{1}{(i (x-i\epsilon ))^\alpha } e^{ikx} dx = |k|^{\alpha-1}{\Gamma(1-\alpha)} \sin (\pi \alpha) (1+ \text{sgn}(k))$$ $f(x)= (-i (x + i \epsilon))^\alpha$인 경우에는 lower half plane($k<0$)에서 적분경로를 선택하면 된다.  $$ \int_{-\infty }^\infty \frac{1}{(-i (x+i\epsilon ))^\alpha } e^{ikx} dx = |k|^{\alpha-1}{\Gamma(1-\alpha)} \sin (\pi \alpha) (1+ \text{sgn}(-k))$$  $\Gamma(\alpha) \Gamma(1-\alpha)= \frac{\pi}{\sin(\pi \alpha)}$임을 이용하면 

$$ \int_{-\infty}^\infty \frac{1}{( \pm i (x \mp i \epsilon ))^\alpha }e^{i k x} dx=   \frac{2\pi |k|^{\alpha-1} }{\Gamma(\alpha) } \theta(\pm k)$$

$$ I = \int_{-\pi/2}^{\pi/2} \cos (a \theta) \cos ^b (\theta) d \theta \qquad \qquad (a>b>-1)$$

먼저 $\cos \theta = (e^{i \theta}+ e^{-i \theta})/2$임을 고려하면 

$$ I = \text{Re} \int_{-\pi/2}^{\pi/2} e^{i a \theta} \left( \frac{e^{i \theta}+ e^{-i \theta}}{2} \right)^2 d\theta$$로 쓸 수 있다. 이는 복소평면에서 $-\pi/2 \le \theta \le \pi/2$인 반원($C_0: |z|=1, -\pi/2\le \arg(z)\le \pi/2$)에서 적분으로 생각할 수 있다. $z= e^{i \theta}$놓으면 $d\theta = dz/iz$이므로

$$ I = \text{Re} \int_\text{right half circle} z^a \left( \frac{z^2 +1}{2z} \right)^b \frac{dz}{iz}= \frac{1}{2^b} \text{Im} \int_\text{right half circle} z^{a-b-1} (z^2+1)^b dz$$ 따라서 $$f(z) = z^\alpha (1+z^2)^\beta \qquad \qquad(\alpha>-1, ~\beta>-1)$$를 그림과 같은 폐경로를 반시계방향으로 순환하는 선적분을 고려하자.

$z=0, \pm i$가 $f(z)$의 branch point이므로 그림에 표시된 cutline을 선택한다. 그러면 $$-\pi \le \arg(z)\le \pi,~-\frac{\pi}{2} \le \arg(z+i),~\arg(z-i) \le\frac{3\pi}{2} $$로 잡을 수 있다. $z=0~(z=\epsilon e^{i \theta})$과 $z=\pm i~(z=\pm i + \epsilon e^{i \theta})$을 감싸는 원호에서 적분의 기여는 없음을 쉽게 알 수 있다. $C_1$에서 적분은 $$ z= y e^{i \pi/2}~~(y: 1\to 0) \\ z+i = (1+y) e^{i \pi/2},~z-i = (1-y) e^{- i \pi/2}$$이므로 

$$ \int_{C_1} =  \int_1^0 y^{\alpha } e^{i \pi \alpha /2} (1- y^2) ^ \beta (e^{i \pi/2} dy) = -e^{i \pi(\alpha+1)/2} \int_0^1 y^{\alpha} (1-y^2)^ \beta dy  $$

$C_2$에서는 $$z=y e^{-i \pi/2}~(y:0\to 1)\\ z+i = (1+y) e^{i\pi/2},~z-i = (1-y) e^{-i\pi/2} $$이므로

$$ \int_{C_2} = \int_0^1 y^{\alpha } e^{-i \pi \alpha/2} (1-y^2)^\beta  (e^{-i\pi/2} dy) = e^{-i \pi(\alpha+1)/2} \int_0^1 y^{\alpha } (1-y^2)^\beta  dy$$

그림의 경로에서 $f(z)$가 analytic하므로 

$$ \oint f(z) = 0 \\  \to~~  \int_{C_0} f(z) dz = - \int_{C_1+ C_2} f(z)dz = 2i \sin \frac{\pi(\alpha +1)}{2} \int_0^1 y^{\alpha}(1-y^2)^{ \beta} dy$$이고 $\alpha = a-b-1$, $\beta=b$이므로

$$ I = \frac{1}{2^b} \text{Im} \int_{C_0} f(z) dz =   \frac{1}{2^b} \sin \frac{\pi(a-b)}{2} \int_0^1 y^{a-b-1} (1-y^2)^b dy$$

$y^2=t$로 치환하면 

$$ I = \frac{\sin \frac{\pi(a-b)}{2}}{2^b } \int_0^1 t^{(a-b)/2-1} (1-t)^b dt $$이고 $\Gamma(z)$의 정의를 사용하면 $$I = \frac{\sin \frac{\pi(a-b)}{2}}{2^b } \frac{\Gamma(\frac{a-b}{2}) \Gamma(b+1)}{\Gamma(\frac{a+b}{2}+1)}  = \frac{\pi }{2^b }\frac{{\Gamma(b+1)}}{{\Gamma( \frac{a+b}{2}+1) \Gamma(\frac{b-a}{2}+1)}}=\frac{\pi}{2^b}\begin{pmatrix} b\\ \frac{a+b}{2} \end{pmatrix}$$여기서 중간 등호는 $\Gamma(m)\Gamma(1-m)=\frac{\pi}{\sin (m\pi/2)}$임을 사용했다. Check

$$ a=1, b=0:~~\int_{-\pi/2}^{\pi/2} \cos \theta d \theta = 2\\ I =\pi \frac{\Gamma(1)}{\Gamma(1+\frac{1}{2})\Gamma(\frac{1}{2}) } = \pi \frac{1}{\frac{1}{2} (\sqrt{\pi})^2} = 2$$

복소함수 $F(z)$의 inverse Z-transform은

$$ Z^{-1} [ F(z)] = \frac{1}{2\pi i} \oint F(z) z^{-n} dz~~~~ (n =0,1,2,...)$$

로 정의되는데, $$F(z) = \left( \frac{z-1}{z} \right)^\alpha ~~~~(\alpha = \text{Real})$$인 경우에 대해 구하자. $z=0$과 $z=-1$이 $F(z)$의 branch point이므로 그림과 같은 dog bone 모양의 경로(반시계 방향)를 선택한다. 

그러면 $ -\pi \le \arg(z), \arg(z+1)\le \pi$로 선택할 수 있다.  $z=0$과 $z=-1$을 감싸는 미소원에서 적분의 기여가 없고, $C_1$에서는 $z= x e^{-i \pi}$, $z+1 = (1-x) e^{i 0},~~(x: 1\to 0)$이므로 

$$ \int_{C_1}  = \int_1^ 0 \left( \frac{1-x}{x} \right)^\alpha e^{ i \pi \alpha } x^{n-1} e^{ -i \pi (n-1)}  e^{-i\pi}dx \\ = -e ^{- i\pi (n-\alpha) } \int_0^1  x^{n-1-\alpha} (1-x)^\alpha dx$$ 그리고 $C_2$에서는 $z= x e^{i \pi}$, $z+1=(1-x) e^{ i \pi},~~(x:0\to 1)$이므로

$$ \int_{C_2}= \int_0^1 \left( \frac{1-x}{x}\right)^\alpha e^{-i \pi \alpha} x^{n-1} e^{i \pi (n-1)} e^{i \pi }dx \\= e^{i \pi (n-\alpha) } \int_0^1 x^{n-\alpha-1 } (1-x)^\alpha dx $$ 따라서

$$ \frac{1}{2\pi i} \oint F(z) z^{-n} dz = \frac{\sin[ \pi (n-\alpha) ]}{\pi } \int_0^1 x^{n-\alpha-1 } (1-x)^\alpha dx $$그리고 Gamma 함수 $\Gamma(z)$를 사용하면,

$$ \frac{1}{2\pi i} \oint F(z) z^{-n} dz = \frac{\sin[ \pi (n-\alpha) ]}{\pi }\frac{\Gamma(n-\alpha) \Gamma (\alpha +1) }{\Gamma(n+1)}$$로 쓸 수 있고, 또 다음 관계

$$ \Gamma (m) \Gamma (1-m)=\frac{\pi}{\sin (\pi m)}$$를 이용하면

$$ \frac{1}{2\pi i} \oint F(z) z^{-n} dz = \frac{\Gamma(\alpha +1)}{\Gamma(n+1) \Gamma (\alpha -n+1)} = \begin{pmatrix} \alpha \\n \end{pmatrix}$$

$$I= \int_0^\infty \frac{ \log x dx }{x^3-1}=  \frac{4}{27} \pi^2$$

함수 $$f(z) = \frac{\log z}{z^3 - 1}$$을 그림과 같은 경로에 적분하자.(참고: https://kipl.tistory.com/670)

$z=0$은 branch point이므로 그림과 같이 cutline을 선택한다. 그리고 $z=1$은 removable singularity이므로 별다른 처리가 필요없고( $\frac{\log x}{x^3-1} = \frac{1}{3} -\frac{1}{2}(x-1) + \frac{1}{2} (x-1)^2 + ... $). $C_\infty$와 $z=0$을 감싸는 $\gamma_1$에서 적분은 0에 수렴한다. $z=e^{i 2\pi/3}  $은 simple pole로 경로 $\gamma_2$처럼 우회한다. 그러면 경로 $\gamma_2$에서 $z= e^{i2\pi/3} + \epsilon e^{i \theta}$이므로 $$ \int_{\gamma_2} =  \int_{2\pi/3}^{-\pi/3} \frac{ \log (  e^{i 2\pi/3}  ) (i \epsilon e^{i \theta} d \theta ) }{ \epsilon e^{i \theta} ( e^{i2\pi/3} - 1)(e^{i2\pi/3}- e^{i 4\pi/3})} = \frac{2\pi^2}{9} e^{i 2\pi/3}$$ $C_1$에서는 $z= x~(x: 0 \to \infty)$이므로 $$ \int_{C_1} f(z) dz = I$$ $C_2 +C_3$에서는 $z= e^{i 2\pi/3} x = e^{i 2\pi/3}x~(x:\infty \to 0)$이므로 $$ \int_{C_2+C_3}  = \int_\infty ^0 \frac{ \log (x e^{i 2\pi/3} )  e^{i 2\pi/3} dx}{  x^3 -1}= - e^{i2\pi/3}\int_0^\infty \frac{\log x +i\frac{2\pi}{3}}{x^3-1}dx\\ =- e^{i 2\pi/3} \left(   I  + i \frac{2\pi}{3} \int_0^ \infty \frac{dx}{x^3-1} \right) =  - e^{i 2\pi/3} \left( I + i \frac{2\pi}{3} J \right)$$ $J = \int_0^\infty \frac{dx}{x^3-1} =- \frac{\sqrt{3}}{9} \pi$ 이므로(https://kipl.tistory.com/670) $$ \oint f(z) dz = 0 ~\to ~(1- e^{i 2\pi/3}) I  -i \frac{2\pi}{3} e^{i 2\pi/3}  J + \frac{2\pi^2 }{9} e^{i 2\pi/3}=0 \\  I = \frac{e^{i 2\pi/3}}{1- e^{i 2\pi/3}} \left( -i \frac{2\pi}{3} J - \frac{2\pi^2}{9} \right) = \frac{4}{27}\pi^2$$ 

$$I = \int_0^\infty \frac{x^{-ia}dx}{ x^2 +x+1} = \frac{2\pi}{\sqrt{3}} \frac{\sinh (\pi a/3) }{\sinh (\pi a)} $$

함수 $$f(z) = \frac{z^{-ia}}{z^2 + z + 1} = \frac{e^{-ia \log z}}{ z^2 + z + 1}$$

$z=0$이 branch point이므로 $+x$ 축을 cutline으로 선택하자. 그러면 $0\le \arg(z)\le 2\pi$. 그리고 $z_1=e^{i 2\pi/3}$, $z_2 = e^{i 4\pi/3}$은 simple pole로 residue는 각각

$$ \text{Res}f(z_1) = \frac{e^{-i a \log e^{i 2\pi/3}}} { e^{i2\pi/3}-e^{i 4\pi/3}} = \frac{e^{2\pi a/3}}{i\sqrt{3}}$$

$$ \text{Res}f(z_2) = \frac{e^{-i a \log e^{i 4\pi/3}}} { e^{i4\pi/3}-e^{i 2\pi/3}} = \frac{e^{4\pi a/3}}{-i\sqrt{3}}$$

$C_1$을 따라 $z= x e^{i0}~(x:0\to \infty)$이므로 

$$ \int_{C_1} = \int_0^ \infty \frac{e ^{-ia \log x} dx}{x^2 + x+1} = I$$

$C_2$을 따라 $z= x e^{i 2\pi}~(x:\infty\to 0)$이므로 

$$ \int_{C_2} = \int_\infty^0 \frac{e^{-ia (\log x+ {i 2\pi}) } dx}{x^2 + x +1} =  - e^{2\pi a} I $$이어서

$$ \int_{C_1 + C_2} = - 2\sinh(\pi a) e^{\pi a} I $$

$C_\epsilon$과 $C_\infty$에서는 0으로 수렴하므로, residue 정리에 의해서

$$  \int_{C_1+C_2} f(z) dz = 2\pi i \times \sum \text{Res}f(z_k) \\       \to~ - 2\sinh(\pi a) e^{\pi a} I = -\frac{4\pi}{\sqrt{3}} e^{\pi a} \sinh \frac{\pi a}{3} \\ \to ~~ I  = \frac{2\pi}{\sqrt{3}} \frac{\sinh(\pi a/3) }{\sinh(\pi a)} $$