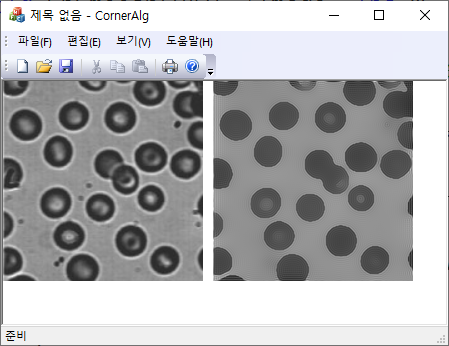
열방정식에서 매질에서 열의 확산은 특별히 선호된 방향이 없이 모든 방향에 대해서 동등하다. 물론 매질의 열전도도가 다르면 국속적으로 열확산이 균일하지 않을 수는 있어도 방향을 따지는 않는다. 그러면 방향에 따라 열의 확산을 정도를 다르게 설정하려면 어떻게 해야 할까? 이는 열방정식을 이용해서 이미지의 smoothing을 하는 필터에서도 동일한 상황이 생길 수 있다. 특히 에지를 보존하면서 smoothing을 할 때 에지에 수직방향으로는 확산이 잘 안일어나게 억제해야 할 필요가 있다. 이를 위해 2차원 열방정식의 우변을 살펴보자. 우변은 온도 $u(x,y;t)$의 Laplacian이 들어오는데 보다 일반적인 Hessian matrix $H$을 써서 표현하면 그 의미가 더 명확해진다.
$$ H = \begin{pmatrix} u_{xx} & u_{xy}\\ u_{xy} & u_{yy} \end{pmatrix}$$
$$ u_{xx} + u_{yy} = (1, 0).H. \begin{pmatrix} 1 \\0\end{pmatrix}+ (0,1) . H. \left( \begin{matrix} 0 \\1 \end{matrix} \right) = \text{Tr}\left ((e_1 \otimes e_1^T + e_2 e \otimes _2^T).H\right)$$
즉, Laplacian은 평면에서 두 단위 벡터 $e_1=(1,0)^T$과 $e_2 =(0,1)^T$ 각각에 Hessian을 작용한 결과를 다시 자신과 내적을 한 값을 동일하게 더하여 나온다. 따라서 $x$방향이나 $y$방향에 무관하게 등방적으로 작용하게 된다. 그러나 $x$방향과 $y$방향에 다른 가중치 $\alpha, \beta\ne \alpha$를 둔다면 등방성은 사라지게 될 것이고 가중치가 큰 방향으로 열의 확산이 더 잘 일어나게 된다.
$$ \alpha u_{xx} + \beta u_{yy}= \alpha \times (1, 0).H. \left(\begin{matrix} 1 \\0\end{matrix} \right)+ \beta(0,1) . H. \left( \begin{matrix} 0 \\1 \end{matrix} \right) = \text{Tr}\left((\alpha e_1 \otimes e_1^T + \beta e_2 \otimes e_2^T).H \right)$$
일반적으로 $x,y$ 방향의 단위벡터 대신에 서로 직각이 단위벡터를 사용해서 비등방성을 줄 수 있다. 예를 들면 에지 방향에 수직한 방향으로 확산을 억제하고 싶은 경우에는 그래디언트의 공변행렬 $\left(\begin{matrix} u_x^2 & u_x u_y\\ u_x u_y& u_y^2 \end{matrix}\right)$의 두 고유벡터 $v_1$, $v_2$를 이용할 수 있다. 이 경우 고유값이 큰 쪽에 해당하는 고유벡터의 방향이 에지에 수직방향이고, 작은 쪽이 에지 방향을 가리킨다.
$$ \text{Tr}\left( (c_1 v_1 \otimes v_1^T + c_2 v_2 \otimes v_2^T ).H\right) = \text{Tr}(T.H) \\T= c_1 v_1 \otimes v_1^T + c_2 v_2 \otimes v_2^T $$
이 경우 비등방적 확산은 텐서필드 $T$에 의해서 제어가 되고 열(확산)방정식은 다음과 같이 간단한 형식으로 표현할 수 있다.
$$ u_t = \text{Tr} (T.H)$$
텐서필드는 고유벡터의 텐서곱을 선형결합해서 만드는데 계수 $c_1$과 $c_2$를 어떻게 선택하는가에 따라 확산의 유형이 달라진다. 에지를 보존하도록 컨트롤하기 위해서는 고유값이 큰 방향으로 가중치가 작게 되도록 선택을 해야 한다. 많이 사용되는 예로는 고유값이 각각 $\lambda_1 < \lambda_2$일 때
$$ c_ 1 = (1 + (\lambda_1 + \lambda_2)/s)^{-p_1}, ~~c_2 = (1+ (\lambda_1 + \lambda_2)/s)^{-p_2}, ~~0<p_1 < p_2$$
로 잡는다.


void AnisoDiffusion(double **image, int width, int height) {
// preparation;
// ....
// main iteration loop
for (int iter = 0; iter < max_iter; iter++) {
// compute gradients;
Gradient(image, width, height, Gx, Gy);
// compute the tensor field T, used to drive the diffusion
for (int x = width; x-- > 0;) {
for (int y = height; y-- > 0;) {
// covariance matrix;
double a = Gx[x][y] * Gx[x][y];
double b = Gx[x][y] * Gy[x][y];
double d = Gy[x][y] * Gy[x][y];
// eigenvalues of symm matrix [a,b;b,d]
double lambda1, lambda2;
Eigenvalues(a, b, d, lambda1, lambda2); // 0 <= lambda1 <= lambda2;
// eigenvector for lambda1; ev1=(u,v);
double u, v;
Eigenvector(a, b, d, lambda1, u, v);
// eigenvector for lambda2: ev2=(-v,u);
double val1 = lambda1 / drange2;
double val2 = lambda2 / drange2;
double f1 = pow(1 + val1 + val2, -a1);
double f2 = pow(1 + val1 + val2, -a2);
// T = f1 * (ev1.ev1^T) + f2* (ev2.ev2^T)
T[0][x][y] = f1 * u * u + f2 * v * v; //(0,0)
T[1][x][y] = (f1 - f2) * u * v; //(0,1)=(1,0)
T[2][x][y] = f1 * v * v + f2 * u * u; //(1,1)
}
}
double xdt = 0.0;
// compute the velocity and update the iterated image
for (int x = width; x-- > 0;) {
int px = max(x - 1, 0);
int nx = min(x + 1, width - 1);
for (int y = height; y-- > 0;) {
int py = max(y - 1, 0);
int ny = min(y + 1, height);
double Ipp = image[px][py];
double Ipc = image[px][y] ;
double Ipn = image[px][ny];
double Icp = image[x] [py];
double Icc = image[x] [y] ;
double Icn = image[x] [ny];
double Inp = image[nx][py];
double Inc = image[nx][y] ;
double Inn = image[nx][ny];
// Hessian matrix of image; H=[Ixx,Ixy;Ixy,Iyy]
double Hxx = Inc + Ipc - 2 * Icc;
double Hyy = Icn + Icp - 2 * Icc;
double Hxy = (Ipp + Inn - Ipn - Inp) / 4;
// veloc = trace(T.H)
veloc[x][y] = T[0][x][y] * Hxx + 2 * T[1][x][y] * Hxy + T[2][x][y] * Hyy;
}
}
// find xdt coefficient
if (dt > 0) {
double max1 = veloc[0][0], min1 = veloc[0][0];
for (int x = width; x-- > 0;) {
for (int y = height; y-- > 0;) {
if (veloc[x][y] > max1) max1 = veloc[x][y];
if (veloc[x][y] < min1) min1 = veloc[x][y];
}
}
xdt = dt / max(fabs(max1), fabs(min1)) * drange0;
} else xdt = -dt;
// update image
for (int x = width; x-- > 0;) {
for (int y = height; y-- > 0;) {
image[x][y] += veloc[x][y] * xdt;
// normalize image to the original range
if (image[x][y] < initial_min) image[x][y] = initial_min;
if (image[x][y] > initial_max) image[x][y] = initial_max;
}
}
}
// clean memories;
};'Image Recognition' 카테고리의 다른 글
| Edge Preserving Smoothing (0) | 2024.02.14 |
|---|---|
| Watershed Segmentation (0) | 2021.02.27 |
| Local Ridge Orientation (0) | 2021.02.21 |
| Contrast Limited Adaptive Histogram Equalization (CLAHE) (3) | 2021.02.15 |
| Fixed-Point Bicubic Interpolation (1) | 2021.01.19 |