Geometry & Recognition

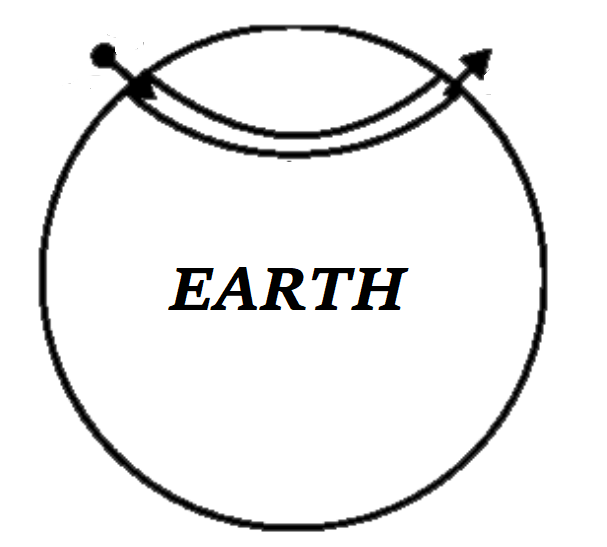
지구 내부(물론 지구는 완벽한 반지름 $R$인 구이고 밀도는 균일하다고 가정한다)에 직선 터널을 뚫어 두 지점을 연결할 때 순수한 중력에 의해서 터널을 통과하는 데 걸리는 시간은 직선 터널의 길이에 상관없이 항상 $T= \pi \sqrt{\frac{R}{g}}=42~\text{min}$로 주어진다. 이는 지표면을 스치듯이 지나는 인공위성의 주기의 절반에 해당한다. 균일한 중력장에서 두 지점을 잇는 직선 경로가 최단 시간 경로가 아니듯 이 경우에도 더 짧은 통과시간을 가지는 경로를 만들 수 있다.

우선 지구 내부에서 질량 $m$인 물체에 작용하는 중력의 세기는 가우스 법칙을 쓰면

$$ \vec{F} =-\frac{GM m} {R^3} \vec {r}= -k \vec{r} = -m \omega^2 \vec{r}, \quad \omega^2 = \frac{GM}{R^3} = \frac{g}{R}$$

처럼 쓸 수 있다(용수철의 탄성력과 같다). 그리고 보존력이므로 위치에너지 함수를 가지는데

$$U(\vec{r}) = \frac{1}{2} m\omega^2 r^2$$

이고 역학적 에너지는 보존된다. 지표면에서 출발을 하면 역학적 에너지는

$$ E= K+U =\frac{1}{2} mv^2 + \frac{1}{2} m \omega^2 r^2 = \frac{1}{2} m \omega^2 R^2 $$

따라서 중심에서 $r$만큼 떨어진 지점에서 물체의 속력은

$$  v= \omega \sqrt{R^2 - r^2}$$

그리고 주어진 터널을 지나는 데 걸리는 시간은

$$ t = \int \frac{d\ell }{v} = \frac{1}{\omega}\int \frac{d\ell }{ \sqrt{R^2-r^2}}$$

터널은 항상 출발, 지구 중심, 도착 지점을 포함하는 한 평면 상에 있어야 하므로 평면 극좌표 $(r, \theta)$를 사용하는 것이 편리하다. 이 경우 터널 곡선은 $r = r(\theta)$로 표현할 수 있으므로

$$ d\ell  = \sqrt{(dr)^2 + (r d\theta)^2} = \sqrt{ r^2 + \dot{r}^2 } d \theta$$

여기서 $\dot{r}= dr/d\theta$를 나타낸다. 터널 통과시간은 따라서

$$ t= \frac{1}{ \omega} \int \sqrt{ \frac{r^2 + \dot{r}^2 }{R^2 - r^2}} d\theta$$

최단 시간을 주는 터널 모양을 찾는 문제는 $t$을 최소시키는 $r(\theta)$를 찾는 변분문제가 된다. 적분인자가 $\theta$에 명시적으로 의존하지 않으므로 Euler-Lagrange 방정식을 써서 

$$ \frac{r^2}{\sqrt{(R^2 - r^2 ) (r^2 + \dot{r}^2)}}=\frac{1}{C} = \text{const} \\ \Longrightarrow \quad \dot{r}^2 = \frac{r^2[(1+C^2)r^2-R^2 ]}{R^2-r^2}$$

임을 보일 수 있다. 중심에서 가장 가까이 왔을 때($\dot r=0$) 거리를 $R_0$라면, $(1+C^2) R_0^2 =R^2$이므로

$$\dot{r}^2 = \frac{r^2\left(\frac{R^2}{R_0^2} r^2-R^2 \right)}{R^2-r^2}$$

모든 거리를 $R$ 단위로 재면 (이 경우 반지름이 1인 행성에서의 터널 문제가 된다) 터널 곡선은 다음 미분방정식을 풀어서 얻을 수 있다.

$$ s = r/R,~~ s_0 = R_0/R, $$

$$ \frac{d s}{d \theta} = \pm \frac{s}{s_0} \sqrt{\frac{s^2 - s_0^2 }{ 1-s^2}}$$

$$ \Longrightarrow ~~\theta = -\int   \frac{s_0}{s} \sqrt{\frac{1-s^2}{s^2 - s_0^2 }}ds $$

적분인자의 root를 벗기기 위해서

$$s^2 = \cos^2 \frac{\phi}{2} + s_0^2 \sin ^2 \frac{\phi}{2}$$로 치환하면 

$$ \theta = s_0 (1-s_0^2) \int \frac{\sin^2 \frac{\phi}{2}}{\cos^2 \frac{\phi}{2}+s_0^2 \sin^2\frac{\phi}{2} }d \frac{\phi}{2} $$

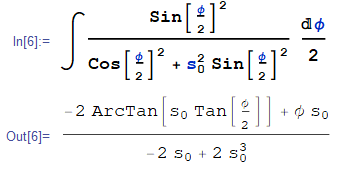
$$\Longrightarrow\quad \theta = \tan^{-1} \left( s_0 \tan \frac{\phi}{2}\right) -\frac{s_0}{2} \phi$$

를 얻는다. 출발지점은 $\phi=0$이고, 중심에서 가장 가까운 지점$(r=R_0)$은 $\phi=\pi$ 그리고 도착지점은 $\phi=2\pi$에 해당한다. 이제 도착시간을 계산하면 

$$t = \frac{1}{\omega} \int  \frac{sds}{\sqrt{(1-s^2) (s^2- s_0^2) }} $$로 쓸 수 있는데 앞의 치환을 이용하면 

$$  t = \frac{1}{2\omega} \sqrt{1- s_0^2} \phi$$

를 얻는다. $\phi= 2\pi$을 대입하면 

$$ t ={\pi}\sqrt{\frac{R}{g}} \sqrt{1-  \left(\frac{R_0}{R}\right)^2}$$

이어서 직선 터널을 움직이는 시간보다 짧다. 그리고 중심을 통과할 때는 ($R_0=0$) 곡선은 직선이 된다. 지구 내부에서 최단시간 곡선은 지구 내부에서 반지름 $r= (R-R_0)/2$인 원을 굴렸을 때 원의 한 지점이 그리는 곡선의 자취로 표현되고, 이 곡선을 hypocycloid라 한다. 이는 직교좌표를 사용하면 더 쉽게 볼 수 있다.

--계속--

Fermat의 원리는 빛이 한 지점에서 다른 지점으로 진행할 때 가장 시간이 적게 드는 경로를 따라 움직인다고 이야기하고 있다. 광속은 굴절률이 큰 곳에서 작아지므로 굴절률이 다른 두 지점을 통과하는 빛의 경로는 되도록이면 광속이 큰 곳을 오래 머무르는 경로를 선택하는 것이 시간상 유리하다. 따라서 매질의 경계면에서 진행방향이 꺾여야 된다. 구체적으로 광속이 $v_1$인 매질에서 $v_2$인 매질로 빛이 진행할 때 입사각  $\alpha_1$,  굴절각 $\alpha_2$인 경우  

$$ \frac{ \sin \alpha_1 }{v_1}= \frac{\sin \alpha_2}{v_2} \quad \Longrightarrow \quad \frac{v} {\sin \alpha} =\text{const}$$을 만족한다. 여기서 $\alpha$는 빛의 진행 방향을 매질 경계면에 수직인 방향에 대해 잰 각이다.

Fermat의 원리는 중력장에서 움직이는 물체에 대해서도 적용할 수 있다. 물체가 움직이면 중력 때문에 속력이 변하게 되므로 두 지점을 잇는 직선을 따라 움직이는 경로는 최단시간 경로가 되지 못한다. 구체적으로 한 지점에서 출발해서 처음보다 아래방향으로 $y$만큼  속력은 역학적 에너지 보존에 의해서 

$$  v^2 = 2gy$$

로 주어진다. 속력이 $y$값이 (아래로) 증가하면 빨라지므로 굴절률이 $\sqrt{y}\sim \sqrt{-U_\text{grav}}$에 반비례해서 연속적으로 감소하는 경우로 생각할 수 있다. 

물체가 움직이는 경로상의 한 지점에서 접선이 수평에 대해 $\theta$만큼 기울어진 경우 입사각은 $\frac{\pi}{2}-\theta$이고, $\cos \theta = dx/ds$이다. 따라서 스넬의 법칙은 (제곱을 해서)

$$ \frac{v^2 }{ \sin ^2(\frac{\pi}{2}- \theta)} = \frac{v^2 }{\cos^2 \theta} = \frac{ 2gy}{(dx/ds)^2 } = \text{const} = 4gr$$

로 쓸 수 있다. $4gr$은 상수이다. 곡선의 미소길이

$$ ds =\sqrt{dx^2  + dy^2 } = \sqrt{1+(dy/dx)^2}dx$$

를 대입하면 중력장에서 물체가 움직이는 최소시간 경로는 다음의 비선형 미분방정식을 풀어서 얻을 수 있다.

$$ \Big( \frac{dy}{dx} \Big)^2 = \frac{2r}{y}-1\quad \Longrightarrow \quad dx = \sqrt{ \frac{y}{2r-y}}dy$$

잘 알려지다시피 이 방정식의 해는 cycloid 곡선으로 다음과 같이 표현할 수 있다. 

$$ x= r(\psi - \sin \psi ), \quad y = r (1- \cos \psi)$$

여기서 $\psi = {\pi-2\theta}$로 주어진다.

변분을 이용해서 구하는 경우는 https://kipl.tistory.com/186

$(1,1)$에서 $(0,0)$까지를 연결하는 일차 곡선 ($y=x$), 이차 곡선 ($y=x^2$), 6차 곡선 ($y=x^6$), 사분원 ($y=1-\sqrt{1-x^2}$) 그리고 cycloid ($x=1-R(\theta-\sin\theta), y=1-R(1-\cos\theta)$) 위를 움직이는 물체의 운동을 mathematica를 사용해서 animation으로 표현하는 방법을 알아보자. 중력가속도는 $g=1$로 놓는다. 적절한 generalized coordinate를 선택해서 Euler-Lagrange equation을 이용하면 운동방정식을 쉽게 구할 수 있다.

(A)  곡선이 $y=f(x)$의 형태로 주어지는 경우 운동방정식은

$$\big[ 1+ (f')^2 \big] \ddot{x} + f' f''  \dot{x} ^2 + f'= 0 .$$

직선경로를 제외하면 운동방정식은 비선형이므로 mathematica의 $\tt NDSolve[]$을 이용해서 수치적으로 푼다.

(B) 원의 경우는 $x$ 좌표보다는 각변수를 이용하면 apparent singularity를 피할 수 있다. 이 경우 운동방정식은

$$ \ddot{\theta} = -\sin \theta,$$

로 주어진다. 

(C) cycloid는 곡선을 따라 움직이는 시간

$$t =\int \frac{ds}{v} = \int  \sqrt{\frac{1 + (dx/dy)^2}{2g(1-y)}}dy$$

을 최소로 만들어주는 곡선이다. cycloid는 다음과 같이 $R$ 변수와 각도 변수 $\theta$로 표현할 수 있다.

$$ 1-x=R(\theta-\sin \theta),~~y-1= -R(1-\cos \theta)$$

이 곡선이 $(0,0)$을 지나야 하는 조건에서 $R$과 그 때의 $\theta$ 값을 구할 수 있다. 먼저 $\theta$을 소거하면,

$$ R \cos \Big( \frac{1+\sqrt{2R-1}}{R} \Big) + 1 = R $$

을 얻고, 이 식의 근을 구하면 $R$ 값이 정해진다. 또한, $$1=R(\theta- \sin \theta)$$을 풀어서 $(0,0)$에 도달할 때 $\theta=\theta_0$ 값을 얻을 수 있다. 그리고 시간과 $\theta$ 변수의 관계는 위의 표현을 적분에 대입하면 

$$t = \sqrt{ \frac{R}{g} }  \theta $$

로 주어짐을 알 수 있다. 이는 사이클로이드가 일정하게 굴러가는 바퀴의 한 점이 그리는 자취이기 때문이다.

아래는 5가지 경우의 곡선 각각에서 운동을 보여주는 mathematica 코드다. 곡선의 모양에 따라 바닥에 도착하는 시간이 다름을 알 수 있다. 출발 높이가 $H$일 때 걸리는 시간은 $\sqrt{H/g}$ 단위로 

직선: $t_1=\int_0^1{ \frac{dy}{\sqrt{1-y}}} = 2$

2차 곡선: $t_2=\int_0^1\sqrt{ \frac{1+4y}{8y(1-y)}}dy= 1.86336$

6차 곡선: $t_6=\int_0^1 \sqrt{\frac{1+36y^{5/3}}{72y^{5/3}(1-y)}}dy=1.90954$

4분원: $t_c=\int_0^{\pi/2} \frac{d \theta}{\sqrt{2\sin \theta }}=1.85407$

cycloid: $t_0= \sqrt{R}\theta_0 = 1.82568$

언덕 꼭대기에서 45도의 직선 경사면 길과 4 분원을 따라 움직이는 경사면 길이 바닥까지 만들어져 있다. 어느 길로 내려오면 더 빨리 바닥에 도달할까?

1. 45도 직선 경사면 길 - 왜냐면 바닥까지 거리가 짧으므로
2. 4 분원 경사면 길 - 처음에 급격히 내려가므로 속력이 급격히 증가하기 때문에

더 빨리 내려올 수 있는 경로가 있을까?

더보기

최단시간 경로를 찾는 문제는 운동시간 $T$의 변분문제로 환원할 수 있다. 우선 최단시간 경로를 $y=y(x)$로 보면 ($H-y\to y$: 내려가는 방향을 $+y$로) Lagrangian 이

$$L= \sqrt{ \frac{1+(dy/dx)^2 }{ y}} $$

일 때 운동방정식의 해를 구하는 문제로 바뀐다. 이 Lagrangian은 $x$에 의존하지 않으므로 Hamiltonian이 일정한 (즉, 에너지가 보존됨) 값을 갖는다.

$${\cal H} = \frac{dy}{dx} \frac{dy/dx}{ \sqrt{y(1+(dy/dx)^2) }} - \sqrt{\frac{1+(dy/dx)^2}{y}}= -\frac{1}{k}=\text{const}.$$

식을 정리하면,

$$ y\left[1 + \left(\frac{dy}{dx}\right)^2 \right] =k^2 \quad \to \quad \frac{dy}{dx} = \pm \sqrt{ \frac{k^2 -y}{y}}$$

을 만족하는 $y(x)$을 구해야 한다. 이 식을 만족하는 곡선이 cycloid이고 $\theta$를 매개변수로 표현하면($r=\frac{1}{2}k^2$),

$$x=r (\theta-\sin \theta), \quad y =r (1 - \cos \theta)$$

이다. 이 경로는 $\theta=0$일 때 $(0,0)$을 지난다. 그림에 맞게 $(0, H)$를 지나고, 감소함수이려면  $y\to H-y$로 바꾸어야 한다. 경로가 다른 끝점 $(H, 0)$을 지나게 하려면 $r$과 그 점을 통과할 때 $\theta_0$ 값을 정해주면 된다. 

$$ x= r( \theta-\sin \theta),~~ y=H- r (1 - \cos \theta)$$ 

이 식에서 $\theta$을 소거하면

$$ H-y + r \cos \frac{x+ \sqrt{ (H-y)(2r-(H-y))} }{r} = r$$을 얻고, 바닥의 $(H,0)$을 통과하려면 $r$은 

$$H+  r\cos \frac{H +  \sqrt{H(2r- H)}}{r} = r$$에서 찾을 수 있다. $H=1$일 때 mathematica을 이용해서 구하면

그리고 $(H,0)$에 해당하는 $\theta$는 $$\theta = \cos^{-1} \frac{r-H}{r}$$에서 $\theta _0=  2.41201$을 구할 수 있다.

그럼 $(0,H)$에서 $(H,0)$으로 내려가는 데 걸리는 시간은? 

$$ds = 2r\sin \frac{\theta}{2}d \theta  ~~\text{and}~~\sqrt{2(H-y)} = 2\sqrt{r} \sin \frac{\theta}{2}$$

이므로

$$ T = \int \frac{ds}{\sqrt{2g(H-y)}}= \sqrt{\frac{r}{g}} \int_0^{\theta_0} d \theta = \sqrt{\frac{H}{g}} \sqrt{\frac{r}{H}} \theta_0 = 1.82568 \sqrt{\frac{H}{g}}$$