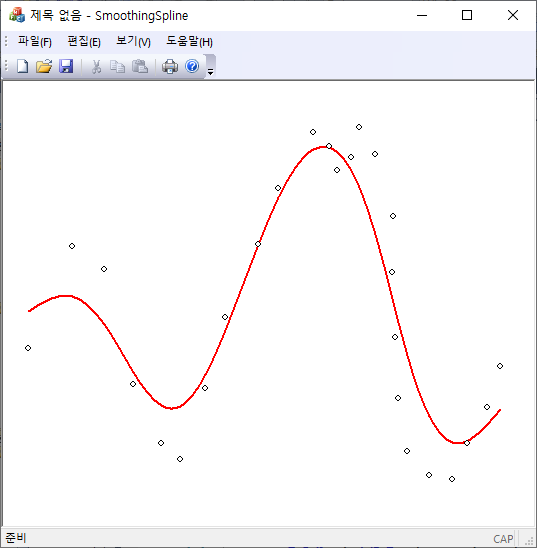
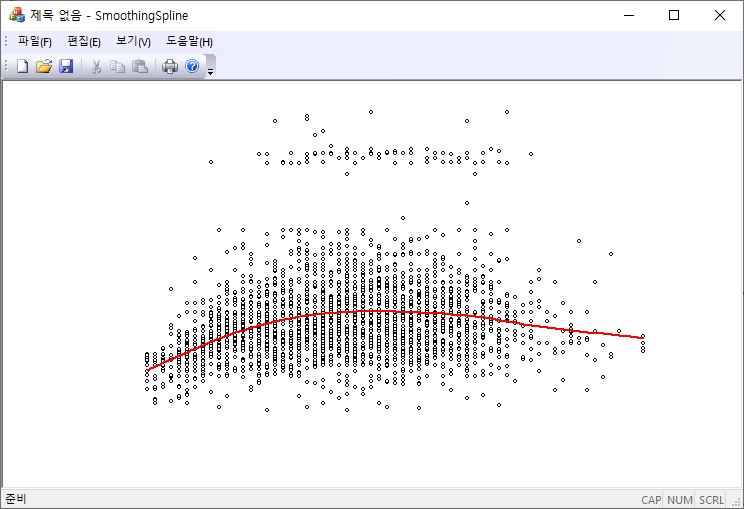
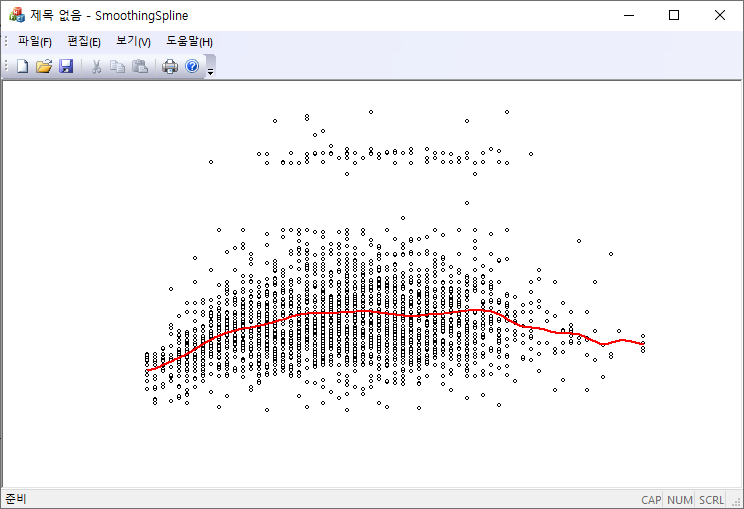
주어진 관측값 $\{x_i, y_i\}$을 spline $y=S(x)$을 이용해서 모델링을 하자. 주어진 관측위치 $x_i$에서 spline은 관측값에 충분히 가까이 지나야 하고, 더블어 관측과 관측 사이에서는 너무 급격히 변하지 않는 곡선이어야 한다. 곡선의 변동은 곡률에 의해서 결정되므로 급격히 변하지 않기 위해서는 spline의 이차 미분값의 크기가 되도록이면 작아한다. 따라서 구하려고 하는 spline은 다음을 최소화시키는 조건에서 찾을 수 있을 것이다.
$$L= \alpha \sum_i \left( \frac{y_i - S(x_i)}{\sigma_i} \right)^2 + \beta \int_{x_0}^{x_n} dx ( S''(x) )^2 \\ S=\underset{}{\text{argmin}}~L$$
여기서 $\sigma_i$는 관측오차에 해당한다. $L$의 두 항은 서로 반대되는 경향으로 spline을 변화시키는데, 첫번째 항이 기여가 큰 경우는 spline이 주어진 관측값의 보간 곡선에 가까워지므로 곡선이 급격히 변할 수 있다. 두번째 항의 기여가 커지는 경우는 spline은 주어진 관측값을 통과하지는 못하지만 충분히 부드러워지게 만든다. 그리고 극단적으로 이 값만 기여하는 경우는 spline은 직선이 되게 된다. 두 항의 상대적인 가중치를 설정하기 위해서 $\beta = 1-\alpha$로 놓을 수 있지만, 첫번째 항과 두 번째 항의 물리적인 차원이 다르므로 단순 비교는 정확하지 않다. 첫번쨰 항은 차원이 없는 반면에 두 번째 항은 거리의 역수 차원을 가지므로 비교를 하기 위해서는 적당한 거리 척도를 곱해 $(1-\alpha)\times\text{distance scale}$로 하는 것이 맞다. 보통 $\alpha=1$로 잡고, $\beta$를 $0$(interpolation에 가까워짐)에서부터 점점 큰 값으로 (직선에 가까워짐)으로 변화시키면 된다.
측정값 사이 구간에서 $n-1$개의 삼차 spline
$$ S(x)=\{ S_i (x) = a_ix^3 + b_i x^2+ c_ix +d_i ,~x_i \le x \le x_{i+1} | i=0,1,2,...,n-1\} $$
을 이용해서 smoothing spline을 구하자. 이 경우 한 구간에서 spline의 미분은 인접 spline 2차 계수의 선형보간으로 표현할 수 있다.
$$S_i''(x)= (1-x/h_i) b_i + (x/h_i) b_{i+1}, ~~h_i = x_{i+1}-x_i$$
따라서 $L$은 다음과 같이 표현된다.
$$L = \alpha \sum_{i=0}^n \left(\frac{y_i - d_i}{\sigma_i} \right)^2 + \beta \sum_{i=0}^{n-1} \frac{4h_i}{3} (b_i^2 +b_i b_{i+1} +b_{i+1}^2 ) $$
따라서 smoothing spline을 찾는 문제는 $L$을 최소화 시키는 $b_i, d_i$을 찾는 문제로 환원되었다. 나머지 계수 $c_i$는 spline의 연속성, $a_i$는 이차 도함수의 연속성을 요구하면 구할 수 있다.
$$ a_i = \frac{b_{i+1} - b_i}{3h_i} \\ c_i = \frac{d_{i+1}-d_i}{h_i} -\frac{1}{3} (b_{i+1}-2 b_i) h_i $$
여기에 1차 도함수의 연속성을 요구하면 $b_i$와 $d_i$사이의 recursion relation을 구할 수 있으므로 최종적으로 $b_i$ 또는 $d_i$을 구하는 문제로 환원이 된다.
$$ b_{i-1} h_{i-1} + 2 b_i ( h_{i-1} + h_i ) + b_{i+1} h_i = \frac{3}{h_i} ( d_{i+1} - d_i ) - \frac{3}{h_{i-1}}(d_i - d_{i-1}) $$
계속...
Ref: https://monoceros.physics.muni.cz/~jancely/NM/Texty/Numerika/CubicSmoothingSpline.pdf
struct Spline {
double x, y;
double a, b, c, d;
double eval(double t) {
return d + (c + (b + a*t)*t)*t;
}
void toBezier(const double h, CPoint Q[4]) {
double xp[4], yp[4];
toBezier(h, xp, yp);
for (int i = 0; i < 4; i++)
Q[i] = CPoint(int(xp[i]+.5), int(yp[i]+.5));
}
void toBezier(const double h, double xp[4], double yp[4]) {
xp[0] = x;
xp[1] = x + h/3;
xp[2] = x + 2*h/3;
xp[3] = x + h;
yp[0] = d;
yp[1] = d + c * h / 3;
yp[2] = d + (2 * c + b * h) * h / 3;
yp[3] = d + (c + (b + a * h) * h) * h;
}
};
void solveFiveDiag(std::vector<double> &u,
std::vector<double> &v,
std::vector<double> &w,
std::vector<double> &q)
{
const int n = u.size();
u[0] = 0; //u[1]은 외부에서;
v[1] = v[1]/u[1];
w[1] = w[1]/u[1];
for (int j = 2; j < n; j++) {
u[j] = u[j] - u[j-2] * w[j-2] * w[j-2] - u[j-1] * v[j-1] * v[j-1];
v[j] = (v[j] - u[j-1]*v[j-1]*w[j-1])/u[j];
w[j] = w[j] / u[j];
}
//forward substitution
q[1] = q[1] - v[0] * q[0];
for (int j = 2; j < n; j++)
q[j] = q[j] - v[j-1] * q[j-1] - w[j-2] * q[j-2];
for (int j = 1; j < n; j++)
q[j] = q[j] / u[j];
// back substitution
q[n] = 0;
// q[n-1]은 외부에서 정해짐;
for (int j = n-2; j > 0; j--)
q[j] = q[j] - v[j] * q[j+1] - w[j]*q[j+2];
}
std::vector<Spline> SmoothingSpline1(
std::vector<double> &x, //n+1
std::vector<double> &y, //n+1
std::vector<double> &sigma, //n+1
double alpha, double beta)
{
const int n = x.size()-1;
std::vector<Spline> S(x.size());
for (int i = x.size(); i-->0;)
S[i].x = x[i], S[i].y = y[i];
std::vector<double> h(n), r(x.size()), q(x.size()), u(n), v(n), w(n);
h[0] = x[1] - x[0];
r[0] = 3 / h[0];
r[n] = 0;
for (int i = 1; i < n; i++) {
h[i] = x[i+1] - x[i];
r[i] = 3/h[i];
q[i] = (y[i+1] - y[i])*r[i] - (y[i] - y[i-1])*r[i-1];
}
//
double mu = 2 * beta / (3 * alpha);
for (int i = 1; i < n; i++) {
double ui = SQR(r[i-1]) * sigma[i-1]
+ SQR(r[i-1] + r[i]) * sigma[i] + SQR(r[i]) * sigma[i+1];
u[i] = mu * ui + 2 * (x[i+1] - x[i-1]);
double vi = -(r[i-1] + r[i]) * r[i] * sigma[i]
- r[i] * (r[i] + r[i+1]) * sigma[i+1];
v[i] = mu * vi + h[i];
w[i] = mu * r[i] * r[i+1] * sigma[i+1];
}
solveFiveDiag(u, v, w, q);
S[0].d = S[0].y - mu * r[0] * q[1] * sigma[0];
double S1d = S[1].y - mu * ((-r[0] - r[1]) * q[1] + r[1] * q[2]) * sigma[1];
S[0].a = q[1] / (3 * h[0]);
S[0].b = 0;
S[0].c = (S1d - S[0].d) / h[0] - q[1] * h[0] / 3;
for (int j = 1; j < n; j++) {
S[j].a = (q[j+1] - q[j]) / (3 * h[j]);
S[j].b = q[j];
S[j].c = (q[j] + q[j-1]) * h[j-1] + S[j-1].c;
S[j].d = r[j-1] * q[j-1] - (r[j-1] + r[j]) * q[j] + r[j] * q[j+1];
S[j].d = y[j] - mu * S[j].d * sigma[j];
}
return S;
}'Computational Geometry' 카테고리의 다른 글
| Alpha Shape (1) | 2024.07.14 |
|---|---|
| Approximate Convex Hull (0) | 2024.06.29 |
| Catmull-Rom Spline (2) (0) | 2024.06.21 |
| Minimum Volume Box (0) | 2024.06.16 |
| Natural Cubic Spline: revisited (0) | 2024.06.14 |