원 내부의 점들은 극좌표 $(r, \theta)$를 사용해서 표현할 수 있다
$$ x=r \cos \theta, ~~y = r\sin \theta .$$
그럼 반지름 $r$을 $[0,1]$ 구간에서 균일하게 선택하고, 각 $\theta$는 $[0,2\pi]$ 구간에서 균일하게 선택하면 원내부에서 균일한 분포를 얻을 수 있을까?
먼저, 원내부에 균일한 점분포가 있을 때 반지름과 각도의 분포가 어떻게 주어질지 알아보자. 이 경우 반지름 $r$ 안에서 점을 발견할 확률(cdf) $P(r)$은 면적에 비례하므로
$$ P(r) =\frac{\text{area}(r)}{\text{area}(1)} = r^2$$
이므로 확률밀도함수(pdf)는 $$p(r) = 2r$$
로 주어진다. 즉, 원내부에서 균일한 점분포는 균일한 각분포를 가지지만, $r$ 분포는 $r \rightarrow1$ 쪽으로 편향되게 된다. 이는 균일하게 $r$을 선택하면 위의 극좌표 변환이 만드는 분포는 원의 중심 부분에 더 집중하는 형태를 가지게 됨을 의미한다.
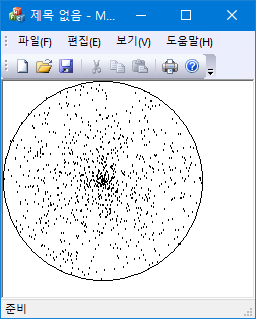
따라서 반대로 균일한 반지름/각 분포를 이용해서 원내부에서 균일한 점분포를 만들려면 $(x, y) \rightarrow (r, \theta)$로 가는 변환의 Jacobian이 상수여야 한다. 위의 결과를 살펴보면
$$ x = \sqrt{r} \cos \theta,~~ y= \sqrt{r} \sin \theta$$
의 변환을 사용해야 Jaconbian이 상수가 됨을 알 수 있다.
$$J = \left| \begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\ \frac{\partial y}{\partial r}& \frac{\partial y}{\partial \theta} \end{array} \right|= \frac{1}{2}$$

void UniformDist_disk(CDC *pDC) {
srand(unsigned(time(0)));
double scale = 100;
for (int i = 0; i < 1000; i++) {
double r = double(rand()) / RAND_MAX;
double ang = 2 * PI * double(rand()) / RAND_MAX;
double x = scale * sqrt(r) * cos(ang);
double y = scale * sqrt(r) * sin(ang);
int xi = int(x + scale + 0.5);
int yi = int(y + scale + 0.5);
pDC->Ellipse(xi - 1, yi - 1, xi + 1, yi + 1);
}
}'Mathematics' 카테고리의 다른 글
| Catenary: constant stress (0) | 2022.01.29 |
|---|---|
| Catenary: Variational Approach (0) | 2022.01.29 |
| Mean distance between two randomly chosen points in unit square (0) | 2022.01.28 |
| Catenary (0) | 2022.01.14 |
| Integration along a branch cut-014 (0) | 2022.01.03 |




