단위구 내의 두 지점을 $\vec{r}_1$, $\vec{r}_2$라면 두 지점이 선택될 확률이
$$ P(\vec{r}_1, \vec{r}_2) = \frac{dr_1^3}{V_1}\times \frac{dr_2^3}{V_1}, ~~~~V_1=\text{volume of unit ball} = \frac{4\pi}{3}$$이므로 두 지점의 사이거리의 평균은
$$ \left< |\vec{r}_1 - \vec{r}_2| \right> =\frac{1}{V_1^2} \iint_\text{unit ball} |\vec{r}_1 - \vec{r}_2| {dr_1^3 dr_2^3} $$
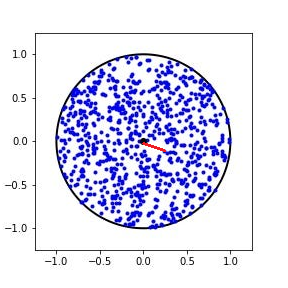
$ \vec{r}_1$과 $\vec{r_2}$의 사이각을 $\theta$라면 고정된 $\vec{r}_1$에 대해서 $\vec{r}_2$의 극좌표의 고도각으로 잡으면 $r_2$ 적분은
$$ I_2 = \int_\text{unit ball} | \vec{r}_1 - \vec{r}_2| dr_2^3$$
$$= 2\pi \int_{0}^1 r_2^2 dr_2 \int_{-1}^1 d \cos \theta \sqrt{r_1^2 + r_2^2 - 2r_1 r_2 \cos \theta } $$
$$= \frac{2\pi}{3} \int_0^{1} r_2^2 dr_2 \frac{(r_1 + r_2)^3 -| r_1 - r_2|^3 }{r_1 r_2 } $$
$$= \pi \left(1 + \frac{2}{3} r_1^2 - \frac{r_1^4}{15}\right)$$
따라서 사이거리의 평균은
$$ \left< |\vec{r}_1 - \vec{r}_2|\right>= \frac{4 \pi}{V_1^2 } \int_0^1 r_1^2 dr_1 \pi \left(1 + \frac{2}{3} r_1^2 - \frac{r_1^4}{15}\right)$$
$$ = \frac{1}{V_1^2} \frac{64 \pi^2}{ 35} = \frac{36}{35}$$
이전 포스팅에서 거리 역수의 평균이 $\frac{6}{5}$임을 보였는데, 평균거리가 이 값의 역수로 주어지지는 않는 점이 의외다.
'Mathematics' 카테고리의 다른 글
| 단위구 내부점간 거리역수의 평균값은? (0) | 2025.02.04 |
|---|---|
| 쌍곡선의 반사특성 (5) | 2025.01.26 |
| 2025 (0) | 2025.01.01 |
| Integration along a branch cut-047 (0) | 2024.12.29 |
| Integrate 1/(1+sin^2 θ) from 0 to 2π (1) | 2024.12.29 |




