Geometry & Recognition

여러 가지 함수를 Fouries series로 재구성할 때 적은 수의 부분합으로도 함수의 원래 모양이 잘 재현되는 경우가 있는 반면에 아무리 많은 항을 더하더라도 재현되지 않는 경우도 있다. 왜 이런 차이가 생기는 것일까? 급격한 모양의 변화가 없는 연속함수에 비해 중간에 값이 점프하는 불연속점이 있는 함수는 Fourier series로 전개를 했을 때 함수의 원래 모양이 잘 재현되지 않는다. 불연속점 전후로 값이 큰 쪽에서는 overshoot가 발생하고, 값이 작은 쪽에서는 undershoot가 발생한다. 이 돌출부는 Fourier series의 부분합의 개수를 늘리더라도 없어지지 않는다. 이처럼 불연속점에서 Fouries series에서 overshoot 또는 undershoot가 발생하는 현상을 Gibbs phenomenon이라 한다. 이는 불연속점에서 직교 고유 함수 전개를 할 때도 나타나는 일반적인 현상이다. 

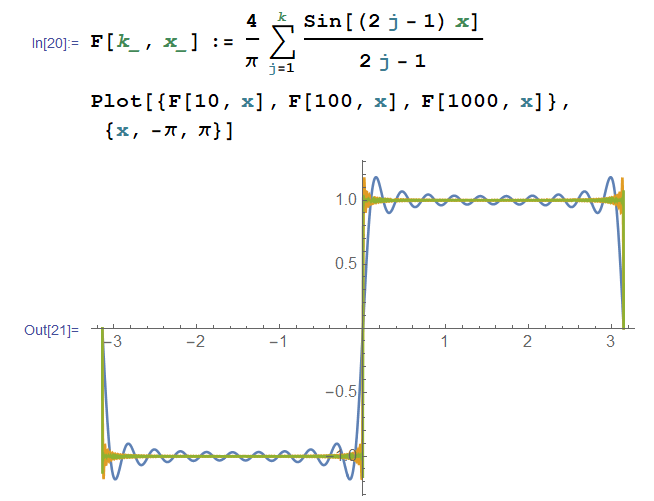
구체적으로 다음 식으로 표현이 되는 square wave

\begin{gather}f(x)=\left\{ \begin{array}{cc}1, &  0<x <\pi \\ 0 , & x=0, \pm \pi \\ -1, & -\pi <x <0\end{array}\right. \end{gather}

을 아래처럼 홀수의 harmonics을 순차적으로 더해서 근사하는 경우를 살펴보자. 

\begin{gather}f_{k}(x) = \frac{4}{\pi} \sum_{j=1}^{k} \frac{ \sin (2j-1)x}{2j-1}=\frac{4}{\pi}\left(\sin (x) + \frac{\sin 3x}{3} + \cdots + \frac{\sin(2k-1)x}{2k-1}\right) .  \end{gather}

$k\to\infty$이면 Fourier 전개에 해당한다. 이 합은 $f(x)$의 불연속점인 $x=0, \pm\pi$을 제외한 영역에서 square wave $f(x)$로 균일하게 수렴한다. 이는 $k$를 증가시키면 불연속점 근방을 제외한 영역에서 부분합 $f_{k}(x)$의 그래프가 square wave의 그래프에 한없이 가깝게 접근함을 의미한다. 그러나 harmonics의 개수를 증가시키더라도 불연속 근방에서 돌출부의 overshoot나 undershoot의 세기는 변하지 않는다. 다만 $k$를 증가시키면 그 폭은 점점 불연속점을 향해 좁아진다. 불연속점$(x=0)$을 기준으로 좌우에서 첫째로 나타나는 극대/극소값의 크기는 $|f(0)+ \frac{f(0^+)-f(0^-)}{\pi} \int_0^\pi \frac{\sin(x)}{x} dx|$로 계산된다. 이 값과 $f(0^\pm)$과의 차이의 절반인 

$$\frac{1}{\pi} \int_{0}^{\pi} \frac {\sin (x)}{x} dx -\frac {1}{2}= 0.0894898\dots$$가 불연속점 $x=0$에서 overshoot나 undershoot의 세기에 해당한다. 이 값은 Wilbraham-Gibbs 상수로 불린다.

Catenary는 여러 가지 놀라운 특징을 가지고 있는데 그중 하나가 포물선을 직선 위에서 굴릴 때 초점이 그리는 자취의 모양도 준다는 점이다. 포물선을 직선 위에서 굴리면 포물선 상의 각 점들은 회전과 동시에 병진 운동을 한다. 포물선의 초점이 어떻게 변화는 보기 위해서 구체적인 포물선을 사용하자. 포물선이 $4a y = x^2$으로 쓰면 초점은 $(0, a)$으로 주어진다. 포물선의 구름을 기술할 때는 매개변수를 사용하는 것이 편리하다. 꼭짓점에 해당하는 매개변수 값을 $t=0$으로 잡으면 포물선의 임의의 점은

$$ (x, y ) = (2a t,  at^2)$$

표현할 수 있다. 굴림에 의해서 포물선 상의 한 점 $(x=2at_1, y=at_1^2)$가 $x$-축 위에 놓이게 되었다고 하자. 이때 회전각은 구르기 전 접선의 기울기에 해당하는 각 $\psi = \tan^{-1}(dy/dx)$ 이다 (그림 참조).

이 과정은 접점 $(x,y)$를 회전축으로 해서 초점의 변위 벡터 $(0,a)^T - (x, y)^T$를(그림의 붉은 화살표)는 시계방향으로 회전시킨 후(왼쪽 녹색 화살표), 원점에서 접점까지의 곡선 길이 $s$만큼 $x$축으로 평행이동시키면 된다(오른쪽 파란색 화살표). 곡선의 길이는 매개변수로 표현하면

$$s= \int_0^{t_1} \sqrt{  (2a)^2 + (2at')^2 } dt' = a(  t_1 \sqrt{1+t_1^2} + \sinh^{-1}(t_1)),$$

이다. 시계방향으로 회전행렬은

$$ \mathbf{R}(\psi) =  \begin{pmatrix} \cos\psi & \sin \psi  \\ -\sin\psi & \cos \psi\end{pmatrix}  ,\quad \tan\psi = \frac{dy}{dx}=\frac{dy/dt}{dx/dt} = t_1 $$

로 표현할 수 있다. 따라서, 이 굴림에 의해서 초점의 위치는

$$ \left(\begin{array}{c} X\\Y\end{array}\right) = \mathbf{R} .\left( \begin{array}{c} 0 - 2at_1 \\ a- at_1^2 \end{array}\right) +   \left( \begin{array}{c} s  \\ 0 \end{array} \right)$$

로 옮긴다. 이를 정리하면 다음 식을 얻는다.

$$ X= a\sinh^{-1}(t_1),\quad Y = a \sqrt{1+t_1^2}$$

이 식에서 $t_1$을 소거하면 초점의 자취가 catenary임을 명확히 볼 수 있다.

$$ Y= a \cosh (X/a)$$

구르는 포물선의 꼭짓점의 자취는 

$$ X=- \frac{at}{\sqrt{1+t^2}} + a\sinh^{-1}(t), \quad Y= \frac{at^2}{\sqrt{1+t^2}}$$

처럼 주어진다. 따라서 초점과 꼭짓점을 알므로 구르는 포물선도 쉽게 그릴 수 있다.

바퀴를 원형으로 만드는 것보다는 네모로 만드는 것이 가공 측면에서 더 쉽다(?). 그러나 네모 바퀴는 중심이 바닥에서 계속 위-아래로 움직이므로 승차감이 떨어진다. 수평 바닥을 움직일 때 무게중심은 바퀴의 대각선이 수직으로 설 때 바닥에서 가장 높고, 한 변이 접할 때 바닥에서 가장 낮으므로, 바퀴 중심이 일정한 높이에서 움직이게 하려면 바닥의 모양을 평평할 수 없다. 바퀴의 무게중심이 출렁거림 없이 움직이기 위해서는 바닥의 모양이 어떤 형태로 주어야 져야 하는지 알아보자.

https://www.youtube.com/watch?v=qFVti39MvX8

우선 바퀴의 한 변의 길이를 $2\ell$로 하자. 그러면 평평한 바닥일 때 무게중심은 바닥에서 최대로 $\sqrt{2}\ell$ 만큼 올라가므로, 바닥을 변형시킬 때 이 높이를 유지할 수 있도록 모양을 선택하고 이때 곡선을 기술하는 $x$ 좌표를 $x=0$으로 잡는다. $x>0$일 때 바퀴의 한 변이 접하는 접점의 좌표를 $(x, y)$라면, 이 점에서 기울기가 $y' =dy/dx =\tan \psi$이므로 접선의 방정식은 ($(X,Y)$로 표현) 

$$Y - y = y' (X - x) $$

로 표현된다. 그리고 바퀴의 중심은 $(x, \sqrt{2}\ell)$에 있음을 알 수 있고, 중심에서 접선에 가장 가까운 점을 $(X_0, Y_0)$라고 하면 그림에서

$$X_0 - x = (\sqrt{2}\ell- y)\sin \psi \cos \psi = (\sqrt{2}\ell- y) \frac{y'}{{1+(y')^2}} ,$$

$$\sqrt{2}\ell - Y_0 = (\sqrt{2}\ell -y) \cos^2 \psi = (\sqrt{2}\ell-y) \frac{1}{{1+ (y')^2}}.$$

임을 알 수 있다. 바퀴 중심에서 접선까지 거리가 $\ell$이므로 이를 두 점 $(x, \sqrt{2}\ell)$, $(X_0, Y_0)$의 사이거리로 표현하면

$$\ell^2  =  (x - X_0)^2 + (\sqrt{2}\ell- Y_0)^2$$

위의 관계를 정리하면

$$ \ell^2 = (\sqrt{2}\ell- y)^2 \left[ \frac{(y')^2}{ (1+ (y')^2)^2}  + \frac{1}{(1+(y')^2 )^2}\right]$$

이므로 곡선에 대한 다음 식을 얻는다.

$$y = \sqrt{2}\ell - \ell \sqrt{1+ (y')^2}$$

한 번 더 미분하면,

$$ y'' = -\frac{1}{\ell} \sqrt{1 + (y')^2}$$

이어서 위로 볼록인 catenary 형태로 바닥이 만들어져야 함을 알 수 있다. 

$y(0)=0$, $y'(0)=1$을 만족해야 하므로 해는

$$ y= \sqrt{2}\ell - \ell \cosh[ \cosh^{-1}(\sqrt{2}) - x/\ell]$$

임을 알 수 있고, 언덕 하나를 넘는 동안 수평이동거리는 $x= 2\ell \cosh^{-1}(\sqrt{2})\approx 1.76275\ell$이다. 중심이 등속운동($dx/dt = v$)을 하는 경우 바퀴의 회전각속도는 ($y'=\tan\psi$)

$$\frac{d\psi}{dt} = v\cos^2(\psi) y'' = -\frac{v}{\sqrt{2}\ell - y}= - \frac{v}{\ell \cosh[\cosh^{-1}(\sqrt{2})- vt/\ell] }$$

이므로 등각속도 운동은 아니다.

Ref: https://my.vanderbilt.edu/stacyfonstad/files/2011/10/squareWheels.pdf

줄에 걸리는 장력을 줄의 단면적으로 나눈 값이 stress ($\sigma = T/A$)는 균일한 줄에서는 일반적으로 일정할 수 없다. 현수선에서 줄에 걸리는 stress를 유지하려면 줄의 단면적을 가변적으로 만들면 가능하다. 이 경우 현수선 중심선의 모양 $y(x)$가 어떻게 주어지는 알아보자. 현수선의 밀도가 $\rho$, 꼭짓점으로부터 떨어진 거리가 $s$인 지점의 단면적이 $A(s)$일 때, 힘의 평형 조건에서 

$$ \sum F_x = T\cos \psi - T_0 = 0 ,$$

$$ \sum F_y = T\sin \psi  -   \int  \rho g A(s) ds = 0. $$

여기서 $T_0$는 장력의 수평성분으로 꼭짓점에서 장력을 의미한다. 위 식에서 $T$를 소거하여 정리하면

$$ y' = \tan\psi = \rho g \int \frac{A(s) ds}{T_0}$$

을 얻는다. stress가 일정하다는 조건 $ \sigma = T/A(s)$에서 $A(s) =T(s)/\sigma  =  T_0/\sigma \cos \psi$로 치환하면

$$ y' =  \frac{\rho g }{\sigma} \int \frac{ds}{\cos \psi}.$$

양변을 $s$로 미분하면 

$$ \text{LHS}= \frac{d}{ds} y' = \frac{dx}{ds} y'' = \frac{1}{ds/dx} y'',$$

$$\text{RHS} = \frac{\rho g}{\sigma} \frac{1}{\cos\psi}.$$

$\tan \psi = dy/dx$ 이므로 $\cos\psi = 1/\sqrt{1+ (dy/dx)^2}$, 그리고 $ds/dx = \sqrt{1+ (dy/dx)^2}$ 이므로

곡선이 만족해야 하는 방정식은

$$ y'' = \frac{\rho g}{\sigma} (1 + (y')^2 )$$

으로 주어진다.

꼭짓점이 $x=0$을 통과하게 선택하면 $y'(x=0)= 0$이므로 위식을 적분하면

$$ y' = \tan \Big( \frac{\rho g}{\sigma} x \Big).$$

꼭짓점이 원점에 있게 좌표를 잡으면, $y(x=0)=0$, 위 식을 적분해서

$$ y = -\frac{\sigma}{\rho g} \log \cos \Big( \frac{\rho g}{\sigma} x\Big) $$

을 얻는다. 꼭짓점 근방에서 위 곡선은 포물선으로 근사된다.

$$ y \approx \frac{\rho g}{ 2\sigma} x^2 + ....$$

https://kipl.tistory.com/352

두 지점 $x=\pm a$에 같은 높이로 고정되어 있는 길이 $L$인 줄이 만드는 곡선 $y(x)$는 catenary라고 불리는 곡선으로 표현됨은 이미 알고 있다. 이를 에너지 관점에서 구하도록 하자. 전체 계의 에너지는 평형상태이므로 줄의 중력 위치에너지만 존재한다. 줄의 선밀도가 $\mu$일 때 중력 위치에너지는

$$ U = \int {g y dm} = \int {g y \mu ds} = \mu g \int_{-a}^{a}  y \sqrt{1+ (y')^2} dx$$

그리고 줄의 길이가 $L$이므로 

$$ L = \int ds =\int_{-a}^{a} \sqrt{1 + (y')^2 } dx $$

따라서 일정한 길이를 가지면서 위치에너지를 최소화시키는 곡선의 모양을 찾아야 하는데 이는 아래의 범함수의 stationary point를 찾는 문제다.

$$ J = \mu g \int_{-a}^{a} y \sqrt{1 + (y')^2} dx + \mu g \lambda \Big( \int_{-a}^{a} \sqrt{ 1+ (y')^2} dx - L\Big) \\ = \mu g \int_{-a}^{a} \left[ y \sqrt{1+ (y')^2} + \lambda \Big( \sqrt{ 1 + (y')^2} - \frac{L}{2a} \Big) \right] dx \\ = \mu g\int_{-a}^{a} {\cal L} dx$$ 

여기서 $\lambda$는 Lagrange multiplier이다. ${\cal L}$이 명시적으로 $x$에 의존하지 않으므로 (first integral of E-L equation)

$$ {\cal L} - y' \frac{\partial \cal L}{\partial y'} = C=\text{const}$$

임을 알 수 있고, 이를 정리하면 다음의 결과를 얻는다:

$$ y' = \sqrt{ \left( \frac{y + \lambda}{C+ \lambda L/ 2a}\right)^2 -1}$$

이 방정식을 바로 적분을 해서 구체적인 해를 구해도 되지만, 여기서는 이 식을 한 번 더 미분하면

$$ y'' = \frac{1}{C+\lambda L/2a} \sqrt{1+  (y')^2} = \frac{1}{k} \sqrt{1+ (y')^2}$$

을 얻는다. 이 식이 현수선을 기술하는 미분방정식임을 이미 앞에서 살펴보았다. 

https://kipl.tistory.com/352