아날로그 신호로부터 디지털 데이터로 바꿀 때 보통 시간당(sound) 또는 공간적 거리당(image) 일정한 횟수로 데이터를 수집한다. 이 비율을 sampling rate이라 한다. 그런데 sampling rate을 바꾸어야 할 경우가 있다. 1초마다 한 번씩 데이터를 모았는데 실제로 0.5초마다 수집된 데이터가 필요가 한 경우에는 기존의 수집된 데이터와 데이터 사이에서 원 아날로그 신호 값을 알아내야 한다. sampling rate을 바꿀 때 기존의 데이터를 이용해서 원 아날로그 신호에서 수집한 것처럼 새로운 데이터를 만들어 내는 과정이 resampling이다. 이미지에서는 원본을 확대하는 up sampling이나 축소하는 down sampling 등이 resampling의 일종이다. resampling을 하기 위해서는 기존 데이터를 이용해서 데이터와 데이터 사이에서의 값을 추정하는 interpolation이 필요하게 된다. 많이 사용하는 interpolation 방법으로는 nearest neighbor interpolation, linear interpolation, cubic interpolation, spline interpolation 등이 있다. 여기서는 cubic interpolation을 이용한 이미지 resampling을 살펴본다.
$x$축 위의 4 점 $x=-1$, $x=0$, $x=1$, $x=2$에서 값이 $p_0$, $p_1$, $p_2$, $p_3$으로 주어진 경우 $0 \le x \le1$ 구간에서 cubic interpolation 함수는
$$ f(x)=ax^3 +b x^2 + cx +d$$
라고 쓰면, 우선 $x=0$에서 $p_1$, $x=1$에서 $p_2$를 지나므로
$$f(0) = d = p_1 $$
$$ f(1) = a + b+ c+d = p_2$$
를 만족해야 하고, 양끝에서 도함수 값은 주변 입력점의 평균변화율로 주면, 다음식을 만족한다.
$$ f'(0) = c = \frac{p_2 - p_0}{2}$$
$$f'(1) = 3a + 2b + c =\frac{p_3 - p_1}{2}$$
이를 이용해서 $a,b,c,d$를 구하면,
$$a= \frac{1}{2}( -p_0 +3 p_1 -3p_2 +p_3)$$
$$b = \frac{1}{2}(2p_0 -5 p_1 + 4p_2 -p_3)$$
$$ c=\frac{1}{2} (-p_0 +p_2)$$
$$d=p_1. $$
따라서 cubic interpolation 함수는
\begin{align} f(x) &=\frac {1}{2}\big(- x^3 + 2x^2 -x\big) p_0+\frac {1}{2}\big(3x^3 - 5x^2 +2 \big) p_1\\&+\frac {1}{2}\big( -3x^3 + 4 x^2 + x\big) p_2 +\frac {1}{2}\big( x^3 - x^2 \big) p_3 \end{align}
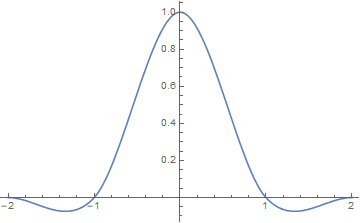
로 쓰인다. 이는 다음처럼 정의된 kernel 함수를(Catmull-Rom filter) convolution한 형태로도 표현할 수 있다.
$$ K(x) = \left\{ \begin{array}{ll} \frac{1}{2} (3|x|^3 - 5|x|^2 +2) & |x| <1 \\ \frac{1}{2}(-|x|^3+5|x|^2 -8|x|+4 ) & 1 \le |x|<2 \\ 0 & \text{otherwise} \end{array} \right. $$
$$ f(x) = p_0 K(-1-x) + p_1 K(-x) + p_2 K(1-x) + p_3 K(2-x),\quad (0\le x <1)$$
여기서는 좀 더 간단히 표현하기 위해서 $$ f(x) = m_0 p_0 + m_1 p_1 + m_2 p_2 + m_3 p_3 $$ 로 표현한다. 물론 $m_i$는 $0\le x <1$의 함수이다. $f(x)$는 그림에서 보는 것처럼 $p_1$과 $p_2$를 통과한다.
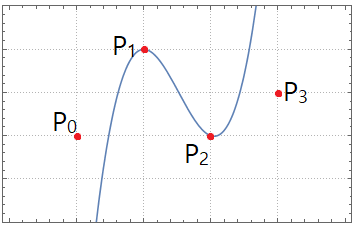
구간 끝에서 도함수를 $$f'(0) = \frac{p_2 - p_0}{2}, ~f'(1) = \frac{p_3 - p_1}{2}$$로 설정했기 때문에 인접 구간(eg. $[p_2,p_3]$)에서의 interpolation과 경계에서 같은 도함수를 가지게 되어 곡선이 꺽임없이 부드럽게 연결이 되는 특성을 가진다(예를 들면, $p_2$와 $p_3$을 보간하는 cubic interpolation함수는 $p_2$에서 미분값이 $(p_3 - p_1)/2$인데, 이는 $p_1,p_2$구간의 interpolation 함수가 $p_2$에서 가지는 미분값과 같다).
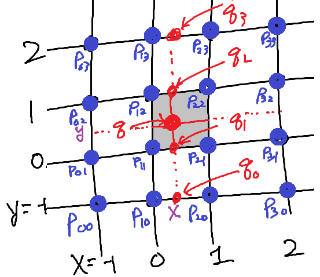
이를 2차원 공간으로 확장하면, 평면 위의 격자점 $\{(x, y)| x, y=-1,0,1, 2\}$에서 16개의 값 $\{ p_{ij} |i, j=0,1,2, 3\}$가 주어진 경우 정사각형 영역 $ 0\le x, y \le 1$에서 bicubic interpolation은 먼저 4개의 행 $y=-1,0,1,2$에서 각각 $x$ 방향의 cubic interpolation 된 값을 구한다:
\begin{align} q_0 =f(x, y=-1)= m_0 p_{00} + m_1 p_{10} + m_2 p_{20} + m_3 p_{30} \\ q_1 =f(x, y=0)= m_0 p_{01} + m_1 p_{11} + m_2 p_{21} + m_3 p_{31} \\ q_2 =f(x, y=1)= m_0 p_{02} + m_1 p_{12} + m_2 p_{22} + m_3 p_{32} \\ q_3 =f(x, y=2)= m_0 p_{03} + m_1 p_{13} + m_2 p_{23} + m_3 p_{33} \end{align}
4개 행에서 구해서 값을 이용해서 다시 $y$ 방향으로 cubic interpolation 한 값을 구하면 bicubic interpolation이 완성된다: $$ q =f(x,y)= q_0 n_0 + q_1 n_1 + q_2 n_2 + q_3 n_3$$ 여기서 $n_i$는 $m_i$에서 $x$를 $y$로 치환한 값이다.
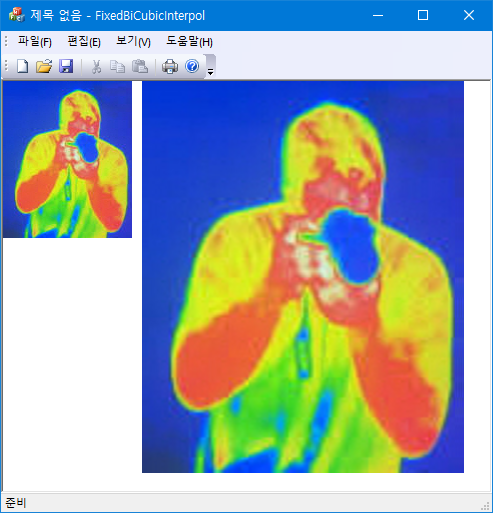
원본 이미지를 확대/축소 또는 변형 등의 변환 과정을 거쳐서 출력 이미지를 만들 때 원본 이미지의 픽셀 값을 resampling 하는 과정이 들어온다. 이때 원본 이미지의 픽셀과 픽셀 사이의 값이 필요한 경우가 발생하여 적절한 interpolation이 필요한데 많이 쓰이는 interpolation 중의 하나가 bicubic interpolation이다. 아래는 bicubic interpolation을 이용한 이미지 resampling을 수행하는 코드다.
interpolation에서 실수(float) 연산을 하지 않고 정수 연산만 사용하면서도 일정한 정밀도로 소수점 아래 부분의 정보를 유지하기 위해 나누기 전에 미리 256을 곱한 후에 나눈다(256 대신에 적당히 큰 수를 선택해도 되는데 2의 지수승을 잡으면 곱셈/나눗셈을 shift 연산으로 대체할 수 있는 장점이 있다). 이렇게 하면 나눈 몫에 $\tt 0xFF$ 비트 마스크를 적용할 때 남는 부분이 소수점 아랫부분을 표현한다. 정밀도는 $1/256$ 까지다. 중간 과정에서 소수점 이하 부분끼리 곱셈을 할 때는 항상 $256$으로 나누어서 $255$ 이하가 되도록 만들어야 한다. 최종 결과에서도 다시 $256$으로 나누기를 해주어야 된다. bicubic인 경우는 $x/y$ 양방향으로 적용하므로 $256\times 256$으로 나누어야 하고 cubic interpolation 계수에서 $1/2$이 들어오므로 추가로 $4$만큼 더 나누어 주어야 한다(코드의 마지막 결과에서 shift 연산 "$\tt >> 18$"이 들어온 이유다).
bicubic interpolation을 적용할 때 $\tt y=0$이나 $\tt x=0$에서는 이전 행이나 열이 없으므로 자신을 반복하는 방식으로 처리해 주어야 하고, 또 $\tt y=rows-2, rows-1$이나 $\tt x=cols-2, cols-1$일 때도 비슷한 처리가 있어야 한다.
int resample_bicubic ( BYTE *src, int cols, int rows,
BYTE *des, int newcols, int newrows ) {
if (cols < 4 || rows < 4)
return resample_bilinear(src, cols, rows, des, newcols, newrows);
int ixn = cols - 4;
BYTE *pa, *pb, *pc, *pd;
for (int j = 0; j < newrows; j++) {
int yy = ( ( j * rows ) << 8 ) / newrows;
int yp = yy >> 8; // src pixel y-position;
int dy = yy & 0xFF;
int dy2 = (dy * dy) >> 8;
int dy3 = (dy2 * dy) >> 8;
int n0 = -dy3 + 2 * dy2 - dy;
int n1 = 3 * dy3 - 5 * dy2 + 2 * 256;
int n2 = -3 * dy3 + 4 * dy2 + dy;
int n3 = dy3 - dy2;
//
pb = src + yp * cols; //current line;
if (yp == 0) pa = pb;
else pa = pb - cols; //previous line;
if (yy < rows - 2) {
pc = pb + cols; //next line;
pd = pc + cols; //next-next line;
} else if (yp < rows - 1) {
pc = pb + cols;
pd = pc;
} else
pd = pc = pb;
for (int i = 0; i < newcols; i++) {
int xx = ( ( i * cols ) << 8 ) / newcols;
int xp = xx >> 8; // src pixel x-position;
int dx = xx & 0xFF;
int dx2 = ( dx * dx ) >> 8;
int dx3 = ( dx2 * dx ) >> 8;
int m0 = -dx3 + 2 * dx2 - dx;
int m1 = 3 * dx3 - 5 * dx2 + 2 * 256;
int m2 = -3 * dx3 + 4 * dx2 + dx;
int m3 = dx3 - dx2;
int p = (xp == 0) ? 0 : (xp < ixn) ? xp - 1: ixn; // p+3 <= ixn+3=cols-1;
int a = ((m0 * pa[p] + m1 * pa[p + 1] + m2 * pa[p + 2] + m3 * pa[p + 3]) * n0 +
(m0 * pb[p] + m1 * pb[p + 1] + m2 * pb[p + 2] + m3 * pb[p + 3]) * n1 +
(m0 * pc[p] + m1 * pc[p + 1] + m2 * pc[p + 2] + m3 * pc[p + 3]) * n2 +
(m0 * pd[p] + m1 * pd[p + 1] + m2 * pd[p + 2] + m3 * pd[p + 3]) * n3) >> 18;
*des++ = (a > 0xFF) ? 0xFF: (a < 0) ? 0: a;
}
}
return 1;
}bicubic interpolation을 하기 위해서는 4점이 필요하므로 폭이나 높이가 이보다 작은 경우는 bilinear interpolation을 사용한다. 다음 코드는 fixed-point bilinear interpolation을 구현한 코드다.
int resample_bilinear(BYTE *src, int cols, int rows,
BYTE *des, int newcols, int newrows ) {
for (int j = 0; j < newrows; j++ ) {
int yy = ((j * rows ) << 8) / newrows;
int yp = yy >> 8; // integer part; src y-position;
int dy = yy & 0xFF; // fractional part;
BYTE *curr = src + yp * cols;
BYTE *next = curr + cols;
for (int i = 0; i < newcols; i++) {
int xx = ((i * cols ) << 8) / newcols;
int xp = xx >> 8; //src x-position;
int dx = xx & 0xFF;
int p00 = curr[xp];
int p10 = curr[xp + 1];
int p01 = next[xp];
int p11 = next[xp + 1];
int val = ((p11 * dx + p01 * (256 - dx)) * dy
+ (p10 * dx + p00 * (256 - dx)) * (256 - dy)) >> 16;
*des++ = val > 255 ? 0xFF: val < 0 ? 0 : val;
}
}
return 1;
}
Bicubic Interpolation
이미지 처리에서 픽셀 좌표는 간격이 1인 2차원 그리드의 교차점으로 볼 수 있다. 이미지를 확대하거나 축소할 때, 픽셀과 픽셀 사이 구간에서 값이 필요한 경우가 생긴다. 간단히는 주변의 가장
kipl.tistory.com
'Image Recognition' 카테고리의 다른 글
| Local Ridge Orientation (0) | 2021.02.21 |
|---|---|
| Contrast Limited Adaptive Histogram Equalization (CLAHE) (3) | 2021.02.15 |
| Distance Transform (0) | 2021.01.16 |
| FFT 알고리즘의 재귀적 구현(a recursive FFT implementation) (0) | 2021.01.14 |
| Edge-Preserving Smoothing (0) | 2021.01.12 |




