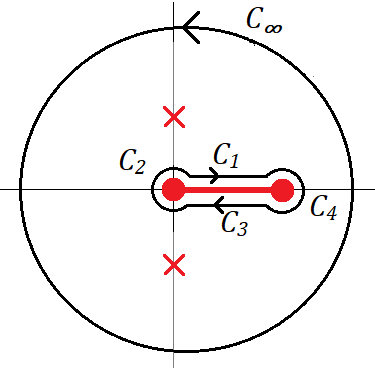
을 그림과 같은 경로에서 적분을 하자.


그러면 residue 정리에 의해서
여기서 branch point 둘레와
그리고
따라서 정리하면 (
'Mathematics' 카테고리의 다른 글
| Inverse Laplace Transform as Bromwich Integral-6 (0) | 2024.11.10 |
|---|---|
| Integration along a branch cut-033 (0) | 2024.11.09 |
| Integration along a branch cut-031 (0) | 2024.11.06 |
| Integration along a branch cut-030 (0) | 2024.11.02 |
| Inverse Laplace Transform as Bromwich Integral-5 (0) | 2024.10.29 |